Arquivos da categoria: Geek

Posts para iniciados em ciência que ainda não completaram seu treinamento Jedi. Estudantes em faculdades de exatas são o que tenho em mente nessas publicações.

No cassino de Parrondo

Geek Rookie

A estatística possui alguns resultados não muito intuitivos, e muito divertidos. Um deles, proposto pelo físico espanhol Juan Parrondo, é um de meus favoritos. Para contar esse aparente paradoxo, convido-os a jogarem um jogo no cassino de Parrondo.

Esse cassino possui duas mesas, uma com um jogo A, outra com um jogo B, que possuem regras diferentes. Em ambos os jogos você só pode apostar uma ficha por vez, digamos, valendo R$100,00. Se você ganhar, leva mais uma ficha consigo. Se perder, perde sua ficha.

No jogo A você deve tirar uma carta de um baralho muito bem embaralhado. Se a carta for preta, você ganha. Se for vermelha, você perde. Neste maço de baralho, contudo, há um curinga; e você perde se tirar o curinga.

No jogo B, as regras mudam um pouco. Se seu número atual de fichas não for um múltiplo de três, suas chances são ótimas: você tira uma carta e perde apenas se ela for de copas ou o curinga. No entanto, se seu número de fichas for múltiplo de três, você deve tirar um às ou o curinga para ganhar, perdendo em todos os outros casos.

Não é surpresa nenhuma se eu te contar que o jogo A é falência na certa. A chance de você perder é maior que a de ganhar, e o ganho é igual à perda; jogar diversas vezes seguidas o jogo A fará você sair do cassino de mãos vazias. E apesar de o jogo B parecer um grande negócio, ele não é, podemos provar com diversas simulações numéricas, o que é o equivalente a jogar várias vezes, que a tendência é perder mais e mais dinheiro jogando o jogo B várias vezes. Assim, nas mesas do cassino de Parrondo a casa sempre vence.

Mas suponha que você pode caminhar de uma mesa à outra. Ora, certamente você só iria ao jogo B quando tem certeza de que suas fichas não são um múltiplo de três; o cassino jamais permitira algo parecido. Então você pode mudar de uma mesa para outra, mas com uma regra: você não pode contar suas fichas. Para deixar ainda mais justo, você não sabe, a cada aposta, se ganha ou perde, fica apenas sabendo o resultado final de suas aventuras ao sair do cassino. Assim, você até pode alternar os jogos, mas, sem contar as fichas e sem saber quando ganha ou perde, não consegue tirar muita vantagem disso. De certa forma, é como se você fosse obrigado a, na entrada, dizer quantas vezes irá apostar em cada jogo e em qual ordem. Assim, nunca sabendo em qual você ganha e qual perde, não poderá mudar de estratégia no meio da noite.

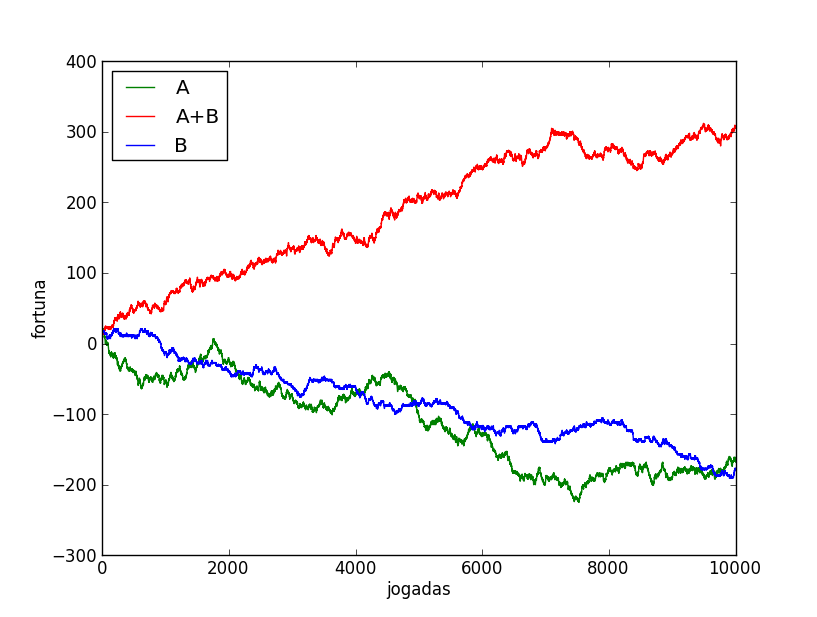
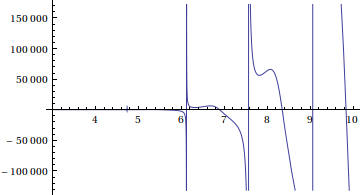
E eis a parte surpreendente. O jogo A é perda certa para você, o B também se jogado continuamente; mas alternar os jogos te leva a ganhar muito dinheiro. Esse fenômeno é o paradoxo aparente de Parrondo, duas táticas fracassadas que, combinadas, resultam em um ganho certeiro. Aos que não acreditam em mim, escrevi um pequeno código de computador para simular esses jogos todos. Claro, um exemplo não prova nada, coloco o resultado apenas para que sua confiança em mim aumente. O jogo A+B consiste em escolher, antes de cada jogada, aleatoriamente um dos jogos, ambos com a mesma probabilidade, como se tirasse no cara-ou-coroa a mesa escolhida para apostar. Eis os resultados, começando com uma fortuna de 47 fichas e permitindo ficar no negativo:

E esse aparente paradoxo nada mais é que um fenômeno estatístico fascinante usado abundantemente em diversos sistemas biológicos, o que inclui suas células. Temos, no caso de Parrondo, um jogo que apenas “bagunça” seu dinheiro (o jogo A, cuja chance é quase 1/2 para cada lado) e outro que te permite ganhar bastante, até atingir um valor (o múltiplo de três) bem difícil de atravessar, tão difícil que é mais fácil o jogo te fazer perder dinheiro a atravessar aquele valor e, perdendo, ele encontrará outro múltiplo de três, e será mais uma vez difícil de subir. No entanto, esse combo “bagunça+tendência” torna-se uma tática interessante, pois a bagunça pode te permitir “saltar” os múltiplos de três e, fora deles, você escala mais fácil a escada da fortuna.

 A partir desse ponto, esse post torna-se geek. Continue por sua conta em risco.

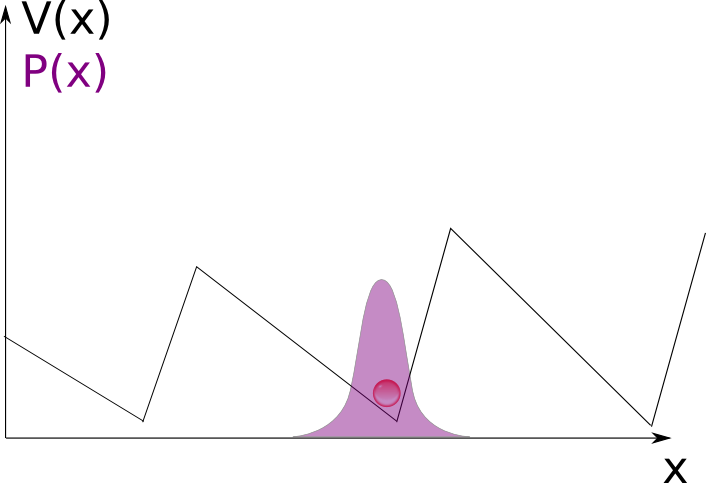
Parrondo não estudava teoria dos jogos, estudava os chamados “motores moleculares”, a base do funcionamento de diversos processos biológicos no nível celular. Suponha uma partícula submetida a um potencial da forma “dente de serra”:

Dente de serra

E suponha essa partícula com uma temperatura suficientemente baixa (ou seja, suficientemente lenta) para que fique confinada no poço. Na figura, o roxo representa a densidade de probabilidade da posição dela, note que é bem difícil ela sair daquele lugar.

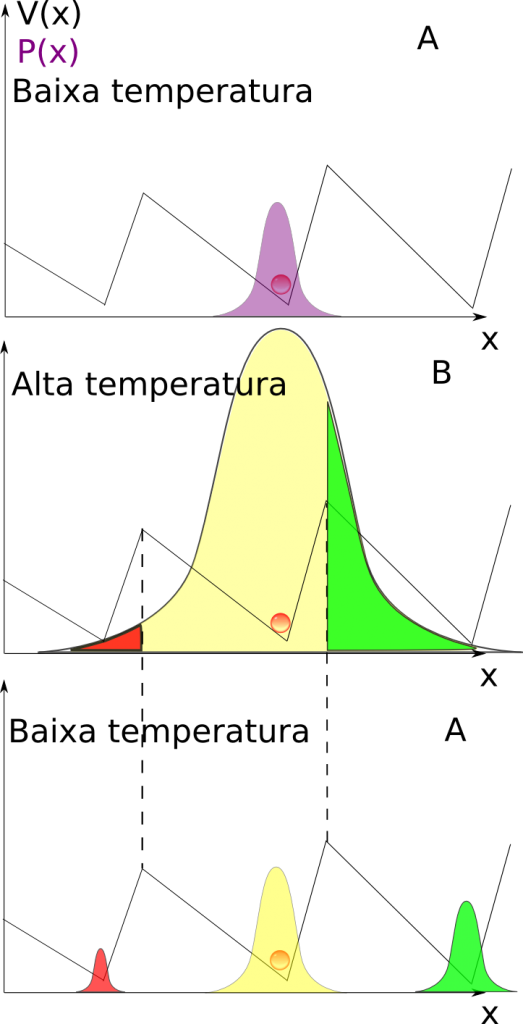
Mas suponha agora que eu aumente bastante a temperatura, bastante mesmo. Ora, a partícula se comportará como se ignorando o potencial, e as chances de ir para a esquerda e para a direita tornam-se as mesmas. Mas algo é diferente, se pensarmos em qual poço é mais provável que ela caia. Veja como é a evolução desse sistema, nessa figura:

parrondo_4

Note que, no momento de alta temperatura, é mais provável que ela tombe no poço da direita (área verde) que no poço da esquerda (área vermelha). Ao resfriarmos o sistema, que é representado pelo terceiro quadro, percebemos que a partícula tende a andar pela serra para a direita. Por causa da assimetria do potencial, o sistema adquire uma direção preferencial.

A relação disso com o cassino é simples, o jogo B é a situação de temperatura baixa e o jogo A é a alta temperatura, andar para a direita significa ganhar dinheiro e perder dinheiro é andar para a esquerda. Mas o cassino de Parrondo é malandro, nele os picos de potencial não são iguais e o jogo B tende a te empurrar para a esquerda, e o jogo A também (o que seria equivalente a uma gaussiana levemente assimétrica). No entanto, pela diferença na inclinação do potencial, passar ao jogo A e voltar ao B torna o sistema mais propenso a te mandar para a direita, a direção de maior fortuna!

Esse jogo de aumento e diminuição de temperatura é a base dos motores moleculares, ele é a razão pela qual a proteína é sintetizada pelo ribossomo em um sentido e não decide, aleatoriamente, seguir o sentido oposto e ir se desfazendo. E a célula funciona, vive, produz e sintetiza proteína dessa maneira: aumento de temperatura, diminuição, aumento (o que deve explicar aquele monte de ATP sendo desfeito para fazer esse sistema andar), em um intrincado maquinário de potenciais assimétricos que nos permite andar, pensar, respirar e jogar cartas em um cassino.

3 respostas

O método científico

Geek

Aprendemos ainda no ensino primário sobre o método científico, e eu até lembro dessa aula. A professora trazia um ovo para a classe e pedia hipóteses sobre o destino do ovo ao ser jogado ao chão. Enumerávamos da mais óbvia à mais absurda, e por fim a professora abandonava o ovo e ele tocava o solo, estava completamente cozido e não fazia sujeira, para entendermos que o método científico é: observação de um problema, formulação de hipóteses, experimento controlado e conclusões.

Tornei-me cientista, pesquiso física, e ganho muitas caras de interrogação quando anuncio a alguém minha profissão. Cientista parece mais profissão de filme, um homem louco em jaleco cercado de vidros coloridos e de poucos amigos. Quando admitem que sou cientista, a próxima pergunta sempre é: “mas o que você faz, exatamente?”. E, para essa pergunta, e para dar uma versão mais real do método científico, listei alguns acontecimentos de um dia meu de trabalho e relato hoje com vocês. Nomeei-o “O método científico”, mas talvez título mais próprio seria “A Day in Life”. Esse post terá alguns detalhes científicos do que faço, é normal alguém de fora da área não os compreender, vou tentar explicar conforme escrevo.

9h30 Chego ao trabalho. Cheguei cedo, não costumo estar aqui antes das 10h, então aproveito para tirar de minha cadeira as coisas que o russo com que divido sala deixou ontem, escrever algo no blog, responder emails, preparar uma caneca de Earl Grey.

10h30 Passei uma hora fazendo o que deveria tomar quinze minutos, é a vida. Abro o Mathematica (programa que costuma fazer contas para mim, mas na realidade é minha cota de autoflagelação semanal). E eis meu problema de hoje: inverter uma transformada de Laplace (o que consiste a uma operação matemática bem difícil). Tento lembrar de minhas aulas sobre essa transformada, a razão de estar usando ela, tudo parece vago e um pouco difícil, vou só mandar o Mathematica fazer: InverseLaplaceTransform[f[s],s,t].

10h45 Mathematica está há quinze minutos na mesma conta, sem me devolver nada, é hora de aceitar a derrota e tentar achar um jeito mais inteligente de fazer isso.

12h Depois de alguma procrastinação com os colegas de laboratório que foram chegando, e depois de ter me forçado a manipular um pouco a forma exata da inversa transformada de Laplace, abandono qualquer esperança de resolver o problema exatamente. A forma exata é bem feia, chama-se integral de Bromwich, e não parece ser um bom caminho. Existem outros métodos, a fórmula de inversão de Post, mas tudo parece fadado ao fracasso, pois a função que quero inverter é, em um caso simples:

\[(100^{-6 – i – j} \Gamma[6 + i + j] \Gamma[-6 – i – j + s] \text{Hypergeometric1F1}[6 + i + j, 7 + i + j – s, 1/100])/ \Gamma[s] + 100^{-s} \Gamma[6 + i + j – s] \text{Hypergeometric1F1}[s, -5 – i – j + s, 1/100].\]

Vou abandonar e tentar fazer isso numericamente.

14h30 Voltei do almoço e parti para o Google buscando métodos numéricos de inversão de Laplace. Descobri como instalar coisas no Mathematica, isso é bem útil. Achei um método bom, chamado Piessens, e ele parece funcionar para funções cuja inversa da transformada eu já conheço (como $\frac{1}{s^2}$).

15h Eis o resultado do Piessens:

O que seria um resultado animador, se o que eu estivesse procurando não fosse uma probabilidade, e ainda não inventaram probabilidade negativa. Há algo errado ou com minha função, ou com o Piessens. Desço e compro um chocolate, preparo outro Earl Grey.

16h Minha função parece boa, o problema é no Piessens, e isso está me deixando nervoso. Durante minha palestra de exposição desse problema, um colega russo (não aquele com que divido sala) perguntou se não valia a pena abrir a série em Taylor e inverter termo a termo, eu respondi que não podia garantir a convergência, mas agora essa ideia parece animadora, tendo em vista a probabilidade negativa.

16h45 Maldito russo, aposto que ele nunca tentou abrir em Taylor e mandar a transformada. Sabe quem é a inversa de Laplace de $x^n$? A n-ésima derivada da delta de Dirac. Agora imagine eu com uma bela coleção de derivadas do delta com coeficientes diferentes para somar, de quê isso me serve? Era para ser uma probabilidade! Veio uma ideia: integrar essa probabilidade para ter a cumulada. Sabe o que acontece? A probabilidade de obter um valor menor que $r$ não depende de $r$ ! E a razão fica evidente uma vez que o método fracassa, só pode ser culpa da inversão da soma com uma operação integral, que pode ser resolvida com o teorema:

Teorema (da convergência dominada de Lebesgue): Ninguém troca integral com limite impunemente.

Vou tentar baixar outro método.

17h15 Achei um, chamado GWR, funciona para funções simples.

18h Eis o resultado com GWR:

E, depois desse gráfico, surge aquele pensamento de “o que estou fazendo com minha vida…?” aliado a uma vontade desenfreada de arremessar o Mathematica pela janela.

18h30 Depressão, seguida de raiva, dá lugar à aceitação. Fim de jogo, vou para casa, amanhã penso em outra coisa. Tento a barganha, ao menos, em um único dia, descobri três maneiras diferentes de não resolver meu problema.

4 respostas

A unicidade do funil

Geek

Um de meus teoremas favoritos, e talvez um dos mais úteis que conheço, é o de Cauchy-Lipchitz. Não só sua demonstração é extremamente divertida, e pode ser vista entre as páginas 23 e 26 deste texto, ele é extremamente poderoso e dá-nos a segurança de afirmar existência e unicidade da solução de diversas equações diferenciais.

Teorema (de Cauchy-Lipschitz). Seja $f=f(y(x),x)$ uma função contínua em $x$ e localmente lipschitziana em $y$ no ponto $y_0$. Seja $y(x_0) = y_0$. Então existe um intervalo $[x_0-\varepsilon, x_0+\varepsilon]$ tal que a equação diferencial

\[\frac{dy(x)}{dx}=f(y(x),x)\]

possui solução única.

Esse teorema é bem forte, já que as condições não são tão exigentes. Todas as funções elementares são contínuas nos pontos de seu domínio, e a condição de localmente lipschitziana, um pouco mais forte, também não é difícil de obter, basta ter uma primeira derivada que não divirja em um dado ponto que a função já é localmente lipschitziana naquele ponto. Em uma explicação grosseira, essa propriedade é o equivalente a exigir um “crescimento controlado” da função, naturalmente funções cujas derivadas primeiras divergem não são nada controladas.

E para provar que toda função contínua cuja primeira derivada não diverge é localmente lipschitziana basta escrever o teorema do valor médio e perceber que ele é exatamente a definição de uma função localmente lipschitziana.

Mas esse post não é sobre resultados da análise real, que são interessantes, mas sobre o problema do funil, conhecido também como clepsidra. Nele, tentamos estudar a velocidade com que a água desce um funil. Chamamos a velocidade no topo da coluna de água $v_A$, sua velocidade na saída de $v_B$, e as superfícies do topo e da saída de $S_A$ e $S_B$ respectivamente. Orientamos a altura no sentido evidente, com a origem na base do funil.

Podemos usar a equação de Bernoulli entre os extremos da água:

\[ \frac{1}{2}\rho v_A^2+\rho gh=\frac{1}{2}\rho v_b^2\]

\[v_A^2=2\left(1-\frac{S_B^2}{S_A^2}\right) gh=2\alpha gh.\]

Notem que eu também usei a equação da conservação da massa, em que $S_Av_A=S_Bv_B$, para isolar a velocidade em A. No final, temos uma equação que relaciona a altura da coluna de água com a sua velocidade:

\[ \frac{dh(t)}{dt}=\sqrt{2\alpha gh}.\]

Para obter uma solução, precisamos de uma condição inicial. E eis o nosso problema. Eu posso dar diversas condições iniciais, valores de $h(t)$, que equivalem à altura da água no instante inicial, mas uma delas, em particular, me incomodará muito: $h(0)=0$. A função $ \sqrt{x}$ não é localmente lipschitziana em zero (notem que a derivada explode, mas a explosão da derivada é apenas condição suficiente, eu teria que provar com mais calma), o teorema de Cauchy-Lipschitz não se aplica a ela se a condição inicial for dada com $h$ valendo zero!

O que é completamente esperado, pois, se eu te contar que agora o funil está vazio ($ h(0)=0$), você não pode me dizer nada sobre a história do funil (obter $h(t)$). Ele pode ter esvaziado há dez segundos (ou seja, $h(-11)$ seria diferente de zero), há três minutos, há horas, dias, pode nunca ter sido cheio (solução $h\equiv 0$); a perda da condição de localmente lipschitziana nos tira a unicidade da solução, e isso é completamente esperado: saber que o funil está vazio nada nos diz sobre quando ele esvaziou!

E essa aplicação curta, bela e tremendamente real do teorema de Cauchy-Lipscitz o torna um de meus favoritos das equações diferenciais, sendo ele já um dos mais úteis. Ao encontrar uma dessas, não hesite, veja a primeira derivada, veja a continuidade, e respire aliviado. Alguma solução existe, e é única. Isso, a um matemático, já é ter a equação quase completamente resolvida, o resto são detalhes.

2 respostas

As condições de Tchebychev

Geek

O post de hoje não é nada longo, mas um resultado que já me ajudou muitas vezes e nunca o vi em outro lugar além de no livro do Demidovich. E como todo o resto desse livro, ele não demonstra, então nunca vi uma justificativa para uma palavra específica daquele resultado, que desde sempre me atormenta. Um dos motivos de não ter encontrado, acho, foi o fato de Tchebychev ser escrito cada vez com uma ortografia diferente, de acordo com os caprichos do autor ou editor, o que escrevo é respeitando a grafia da tradução que tive do Demidovich.

Aos que não conhecem o livro, ele é um monstro russo de mais de mil exercícios espalhados pelas matérias de cálculo, é como uma tábua de multiplicação para o cálculo diferencial, um excelente treinamento de Kumon a quem quer ficar rápido nessas coisas. Ainda, nele encontrei um resultado simples e bem interessante, que hoje compartilho convosco.

Integrando funções na mão, sempre podemos nos deparar com a possibilidade de estar tentando realizar o impossível: encontrar uma primitiva a uma função que não possui primitiva. Poucos cursos de cálculos dão a devida atenção a essa diferença: primitivização e integração não são a mesma coisa. Enquanto é famoso o fato de que nem toda função integrável possua primitiva ($e^{-x^2}$ é o exemplo mais clássico), encontrar uma função F que derivada dê f (o processo de primitivização) não garante que a função seja integrável, apesar dos rumores. Esse exemplo no link é um pouco trabalhoso, e bem poderoso, é uma função com primitiva que não é integrável em lugar nenhum, um contra-exemplo bem interessante.

Mas não consigo me lembrar de nenhum teorema que consiga me dizer quando uma função possui ou não primitiva elementar, ou seja, quando vale a pena sair tentando transformações, integrações por partes ou separações de polinômios em uma função que não me dá chance de integrar, que não possui uma primitiva suficientemente simples para ser encontrada com minhas técnicas baratas de cálculo I. E as condições de Tchebychev são o único teorema desse tipo que já vi:

Condições de Tchebychev: Seja a integral:

\[\int x^m(a+bx^n)^pdx\]

Então esta integral pode ser expressa por meio de uma combinação finita de funções elementares somente nos seguintes casos:

  1. Quando $p$ é inteiro.
  2. Quando $\frac{m+1}{n}$ é um número inteiro. Nesse caso, use a substituição $a+bx^n = y^s$, onde $s$ é o denominador de $p$.
  3. Quando $ \frac{m+1}{n}+p$ é um número inteiro. Nesse caso, use a substituição $ ax^{-n}+b = y^s$, onde $s$ é o denominador de $ p$.

A palavra que me intriga nesse resultado é o somente, pois nunca vi teoremas ou lemas com manobras para provar que uma função não possui primitiva elementar, mas isso provavelmente é ignorância minha. Apesar de não conhecer as engrenagens desse teorema, o resultado é bem útil, e salvou-me a vida vez ou outra, possuindo um ar de mistério que, apesar de me incomodar, ainda me encanta um pouco.

2 respostas

Prova surpresa

Geek Hardcore Rookie

O post de hoje não é muito informativo, é mais perturbador, um probleminha de lógica para não deixar você dormir.

Um professor chega à aula e avisa sua classe que aplicará, no mês de abril, uma prova surpresa. Um aluno, que futuramente se tornaria matemático na área de lógica, pergunta o que o professor entende por surpresa. Estranhando a pergunta, o professor responde que uma prova surpresa é uma prova tal que, no início de cada dia do mês de abril, os alunos não podem deduzir ou saber que a prova será aplicada naquele dia. Triunfante, o aluno conclui que não haverá prova nenhuma, pois:

– Se a prova não for aplicada até o 30 de abril, então ela terá que necessariamente ser nesse dia e, no começo do dia, já não será surpresa. Então o 30 de abril não pode ser a data da prova.

– Se a prova não for aplicada até o 29 de abril, então ela terá que ser necessariamente nesse dia, pois o 30 está excluído. Mas, assim sendo, ela não será uma surpresa, então o dia 29 não pode ser o dia da prova.

– Se a prova não for aplicada até o 28 de abril, então ela terá que ser necessariamente nesse dia, pois o 30 e o 29 estão excluídos. Mas, assim sendo, ela não será uma surpresa, então o dia 28 não pode ser o dia da prova. E assim por diante, ele exclui todos os dias.

No dia 12, ele recebe a prova. Onde ele errou?

7 respostas