Arquivo da tag: Probabilidades

Posts sobre teoria de probabilidades.

Amigo secreto

Geek

Inspirado nesse clima de fim de ano, pensei em problemas que combinariam com essa última semana, e nenhum me pareceu mais adequado que o do amigo secreto. Todos já participamos de algo parecido, você é obrigado a tirar aleatoriamente um amigo que, via de regra, você mal conhece e deve comprar a ele um presente de até um determinado valor. É uma excelente oportunidade de ter que comprar coisas para quem não conhece e receber algo pífio de quem não gosta, porque presentes dependem do presenteado e, com pouca informação a respeito, esse processo tende a receber uma camiseta tamanho M que nunca na vida você usará.

Mas estes não são os únicos problemas do amigo secreto, há outros, que ao menos têm solução. Vou propor duas perguntas sobre a brincadeira, que envolvem pequenos defeitos que podem acontecer na seleção. Encontrar suas soluções é um interessante exercício de combnatória.

1) Qual a probabilidade de alguém tirar a si mesmo?

A primeira pergunta parece simples, mas tanto está longe de ser que ganhou um nome: o problema do chapeleiro. Suponha que o responsável por uma chapeleira perdeu o livro que dizia o dono de cada chapéu. Sem saída, ele distribui aleatoriamente os chapéus a quem vem buscar o seu. Qual a probabilidade de ele não ter acertado nenhum?

A resposta, apesar de bonita, não tem demonstração simples. Se peco na precisão, é por amor à clareza, vou tentar explicar o princípio desse cálculo. Você sabe que todas as permutações possíveis dos chapéus são $N!{}$, onde $N$ é o número de chapéus. Para saber a probabilidade de isso não acontecer, calculamos a chance de acontecer e tomamos a complementar. Para tal, basta somar as permutações que mantêm alguém constante (alguém recebeu o chapéu errado). Mas teremos um problema com isso, como veremos.

  • Missão: calcular a chance de alguém ter recebido o próprio chapéu.

Sabemos que para calcular a chance de uma pessoa $i$ receber seu próprio chapéu basta somar quantas permutações de chapéu resultariam em ele terminando com seu chapéu na mão, e essa conta é simples, são $(N-1)!{}$ (com o dele fixo, calculamos as permutações dos demais). Mas não podemos apenas somar esse número para todos os $i$, pois estaremos contando muitas coisas duas vezes! Para entender, uso de exemplo os quatro irmão, G, B, R e Y, que decidiram ir a uma festa deixando seus chapéus na chapelaria. Eles chegaram da seguinte forma:

hats2

Há $4!=24$ configurações possíveis de distribuição de chapéus na saída, mas há apenas 6 configurações em que o verde recebe seu chapéu corretamente, vejamos:

hats1

Note que seria ingênuo apenas somar essas configurações para todos os irmãos e dizer que esse seria o número de permutações em que alguém recebe seu chapéu corretamente, pois notamos que poucas são as vezes em que apenas o verde recebe seu chapéu, ou seja, na conta do verde há vezes em que outros recebem seu chapéu e essas configurações serão contadas novamente na vez desses outros que receberam o chapéu correto. Felizmente isso pode ser corrigido, basta retirar o número de vezes em que dois recebem os chapéu correto.

Vamos colocar isso em uma linguagem matemática decente. Chamaremos $A_n$ o conjunto das permutações tais que o número $n$ recebe seu chapéu correto. Sabemos que $|A_n|=(N-1)!{}$. Mas o que queremos é $|\cup_n A_n|$, ou seja, o número total de permutações em que alguém é fixo.

Começamos calculando $\sum_n |A_n|$, mas provamos que contamos muita gente duas vezes. Pegamos esse resultado e subtraímos $\sum_{i<j} |A_{i,j}|$, onde $A_{i,j}$ é o conjunto das permutações que deixam $i$ e $j$ fixos, ou seja, eles recebem o chapéu correto.

Agora sofremos de outro mal, o remédio causou um novo sintoma. Ao excluirmos todos os que possuem dois fixos, excluímos duas vezes aqueles que possuem três fixos, e assim por diante, pois eles foram contados mais de uma vez nessa subtração. Isso não é problema, basta colocarmos de volta esses elementos, somando ao resultado o fator $\sum_{i<j<k} |A_{i,j,k}|$. O problema é que nessa soma contamos duas vezes os que possuem quatro fixos.

Deu para entender o mecanismo. Felizmente, como há um número finito de chapéus, ele algum dia terminará. E sabemos que o número de permutações possíveis com $n$ chapéus fixos é $(N-n)!{}$, isso nos permitirá calcular a soma total. Mas precisamos também lembrar que ao calcularmos $\sum_{i<j<k}|A_{i,j,k}|$, por exemplo, temos que somar $(N-3)!{}$ um número de vezes equivalente ao número de configurações possíveis na escolha de $i,j,k$, ou seja, um número ${N\choose 3}$ de vezes. Calculando ${N\choose 3}(N-3)!{}$, abrindo a fórmula binomial, nos resta apenas um fator, nesse caso, de $\frac{N!}{3!}$. É fácil deduzir que com os demais será a mesma coisa:

\[|\cup_n A_n|=\sum_n|A_n|-\sum_{i<j}|A_{i,j}|+\sum_{i<j<k}|A_{i,j,k}|+\ldots\]

\[= \frac{N!}{1!}-\frac{N!}{2!}+\frac{N!}{3!}+\ldots = N!\sum_{j=1}^{N-1} (-1)^{j+1}\frac{1}{j!}$

Esse é o número total de configurações em que alguém recebe seu chapéu corretamente. Para descobrir a chance de alguém receber o chapéu, basta dividir esse valor pelo número total de configurações, ou seja, $N!{}$. Concluímos aquela missão estabelecida acima, mas queremos a chance do complementar acontecendo, e para encontrar a probabilidade de ninguém ter o chapéu correto basta tomar 1 e subtrair esse valor calculado. Teremos:

$P(N)=1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}+\ldots +(-1)^N\frac{1}{N!}$

E essa é a probabilidade, no amigo secreto, de ninguém tirar a si mesmo:

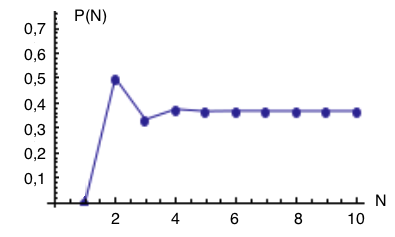
hat_check_graph

É fácil perceber que essa soma tende rapidamente a $\frac{1}{e}$, pois nosso resultado são exatamente as somas parciais da série de Taylor de $\frac{1}{e}$, e é interessante perceber como esse valor já é quase exato já a partir de cinco participantes, a convergência do fatorial sempre impressiona. Como toda boa série de Taylor, o erro é da ordem do último termo somado, então é natural que a partir de 5 participantes a diferença entre essa probabilidade e $ \frac{1}{e}$ seja menor que 1/120. É notável também o fato de, com apenas um participante, a chance ser zero de ninguém tirar a si mesmo, o que era, pelo bom senso, esperado.

O resultado é interessante também por outro motivo. Se aumentamos o número de participantes, a chance de uma pessoa escolhida tirar a si própria é cada vez menor, mas o número de pessoas que podem tirar a si mesmas aumenta, a resposta de “para onde vai a probabilidade” não é trivial e é bem interessante que nenhum desses elementos domine o outro, ou seja, a probabilidade não vai nem para zero, nem para um, mas para um valor intermediário e longe de ser evidente.

2) Qual a chance da brincadeira do amigo secreto não para no meio, ou seja, não “fechar o ciclo” antes de terminar e alguém ser obrigado a recomeçar o jogo?

Essa resposta é mais simples e possui menos imagens. Começamos por um participante qualquer. Para que o jogo não pare, ele não pode tirar a si mesmo, sobram $N-1$ opções. Ao tirar algum deles, essa próxima pessoa não pode tirar nem ela mesma, nem o primeiro, então sobram apenas $N-2$ opções a ela. Assim sucessivamente, é fácil ver que o número de ciclos possíveis que não serão interrompidos será de $(N-1)!{}$. Naturalmente, basta apenas dividir pelo número total de permutações, $N!{}$, para ter a probabilidade de isso acontecer, e ela é $\frac{1}{N}$. Como esperado, quanto maior o grupo de pessoas, mas difícil é obter uma configuração que forneça um jogo sem interrupções.

Depois desse post de combinatória um pouco árido, termino desejando a vocês um excelente ano novo, boas férias e todas as permutações possíveis daqueles votos de fim de ano que não canso de lhes desejar, mas que cansaria de escrever.

Deixe um comentário

Crime e castigo

Rookie

Há algum tempo, inspirado em um comentário desse blog, queria escrever algo sobre o fenômeno estatístico conhecido como regressão à média. Desde pequeno fui fascinado pela análise teórica do sermão que recebia de meus pais a cada travessura que aprontava. Quebrei janelas, copos, sujei-me, sujei a casa, nada voluntário, coisa de criança; mas recebia, a cada evento, a devida repreensão de pai ou mãe (ou dos dois, não eram excludentes). Também levava broncas por notas mais baixas, não tantos elogios pelas altas, que eram, afinal, minha obrigação. Achava que as coisas eram daquele jeito, que não poderia ser de outro jeito, até, entrando na faculdade, conversar com um amigo que cursava administração de empresas. Segundo ele, muito mais eficaz que esse método era o inverso, o tal do positive reinforcement, elogiar o que é bom e trabalhar no que está ruim, mostrar ao time vídeos com seus acertos ao invés de erros, meu amigo citava experiências sociológicas e psicológicas bem interessantes para provar seu ponto, mas eu custava a acreditar.

Dizer que a recompensa é o melhor caminho choca nossa experiência. Estamos habituados a ver resultados melhorarem após a repreensão, e muitos dizem que, após o elogio, o elogiado tende a piorar e a decepcionar, como se elogiar estragasse, como se ficar feliz e orgulhoso o tornasse relaxado. O post de hoje serve para desarmar esse argumento, e nossa ideia de que alguém “aprendeu a lição” após uma bronca bem tomada. Vou argumentar que esse fenômeno de fato existe, a piora em relação ao elogio e a melhora em relação à bronca, mas que ele reflete muito mais uma verdade estatística que uma mudança de comportamento.

Vamos imaginar uma criança, Denis, o pimentinha, que, ao decorrer do ano letivo, fará 20 provas. Ele não é o melhor da sala, nem o pior, e estuda um pouco para cada prova, mas não muito. Denis estuda suas matérias para tirar um 7,0, que é uma nota boa em sua opinião. No entanto, algumas vezes a prova é mais fácil, ou mais difícil, então sua nota varia; sua média é constante, mas as flutuações são aproximadamente de dois pontos em sua nota. Ou seja, vamos tratar a nota de Denis como uma variável aleatória de média 7,0 e distribuição normal com variância 1. Dessa forma, a chance de ele tirar acima de 9,0 é de 2,2%, e a chance de tirar abaixo de 5,0 também é de 2,2%, sendo 68,2% a probabilidade de ele tirar entre 6,0 e 8,0.

Esses números podem parecer estranhos, mas esse modelo é um dos mais adequados para representar tarefas humanas, a chamada distribuição gaussiana, ou distribuição normal. Ela diz que teremos um valor esperado (no caso de Denis, 7,0), mas que teremos dias bons e ruins. A maior parte dos dias (68,2%) não será muito longe do valor esperado (entre 6,0 e 8,0), mas alguns, excepcionais (2,2%), podem ser muito bons (acima de 9,0, caiu exatamente o que ele havia estudado!) ou muito ruins (abaixo de 5,0, não caiu quase nada do que ele sabia).

Sua mãe se preocupa com sua educação, e o disciplina como sua mãe a disciplinou. Ela dá um presente a Denis cada vez que ele tira uma nota acima de 9,0, e o castiga cada vez que ele tira uma nota abaixo de 5,0. Vejamos como seriam as notas de Denis em um ano:

O que a mãe de Denis entenderá desse gráfico? Note que toda vez que ela castiga Denis, suas notas tendem a subir, enquanto toda vez que ela o presenteia, ele tende a tirar notas piores! É importante notar que isso nada diz sobre o aprendizado de Denis, eu apenas tirei notas aleatoriamente, dizendo que Denis é um aluno nota 7,0 que tem dias bons e ruins.

Essa ilusão da eficácia do castigo ocorre porque é muito raro ter dois dias ruins seguidos, e a ilusão da ineficácia do elogio é pela também raridade de dois dias excepcionalmente bons. O valor seguinte ao de um dia excepcional tende a ser menos espetacular, ou, como dizemos, tende a regredir à média dos valores.

Note, eu não estou dizendo que o castigo tem eficácia zero no comportamento, ou que o presente também não tem efeito, estou apenas dizendo que o raciocínio de punir e melhorar e não elogiar para não estragar pode ser aplicado até a variáveis aleatórias. Certamente a maneira como uma pessoa é tratada influencia em sua performance, mas uma teoria de castigo e recompensa que pode ser explicada pelo mero acaso, pela estatística, não pode ser tida como uma grande verdade sobre o comportamento humano.

Em outras palavras, imagine-se alguém que considera tirar menos que 5 em um sorteio para o próximo número do bingo algo ruim, e que considera tirar mais que 95 um resultado bom. Você pode, por algum motivo, culpar aquela esfera engradeada que vomita os números pelo resultado, e eu garanto: se você der uma bronca nela após cada resultado menor que 5, ela vai muito provavelmente melhorar bastante na próxima vez. Se você elogiar a cada resultado acima de 95, ela provavelmente irá te decepcionar na próxima bola sorteada.

Não quero, nem pretendo, dizer que broncas são ineficazes, ou que a única resposta possível para educar ou ensinar são elogios, paz e amor. Lanço esse post na polêmica opinião que pede uma revisão de nossos conceitos da eficácia do castigo como aprendizagem. Para que você se pergunte quanto do que você aprendeu veio dos benefícios de um sermão, ou, ainda, quanto de cada melhora que viu após uma bronca foi resultado dessa bronca ou se foi, por puro acaso, um dia melhor que ontem.

2 respostas

Banco Imobiliário

Geek Rookie

Como todos, joguei bastante Banco Imobiliário em minha infância. Sonhava em morar em Morumbi ou Interlagos, tinha medo de algum dia passar perto da Av. Presidente Vargas, e com ele descobri o significado da palavra “revés”. Gostava, ainda que nunca tenha efetivamente terminado uma partida, sempre me solidarizava com os que empobreciam, deixávamos que continuassem, como se capitalismo e misericórdia combinassem, não dava certo.

Mas sempre fui assombrado pela busca pela tática ótima de se jogar esse jogo, se havia alguma. Inspirado em um estudo que li recentemente, dedico esse post a responder a grande pergunta: quais as casas em que mais paramos em uma partida? Assim, saberemos quais cores de propriedades precisamos, a todo custo, comprar ao parar.

Apesar de esse estudo já ter sido feito, não gostei da apresentação, nem da maneira como foi escrito; refaço-o, torcendo para que poucas pessoas achem, desse post, o que achei do estudo.

Para explicar como farei esse cálculo, preciso começar com um caso mais simples de jogo. Se Quico criou o xadrez para principiantes, apresento a vocês o Banco Imobiliário para iniciantes, ou, para criar uma temática, o Banco Imobiliário Zona Leste, referente à zona leste da cidade de São Paulo (figuras de Pedro Vergani, o mesmo que fez o banner do blog e diversas outras figuras desse blog):

Não há grandes surpresas nesse jogo. Usamos uma moeda e tiramos no cara-ou-coroa quantas casas andaremos: cara nos faz andar uma casa, coroa nos faz andar duas casas. Queremos analisar qual a casa mais provável de se cair e, para isso, precisamos trazer artilharia pesada da álgebra linear.

Vou precisar de uma matriz. Adoro matrizes, trabalho com elas e revolto-me com alunos de colegial que desdenham das aulas em que tiveram que aprender a “multiplicar tabelas”. Não os culpo tanto assim, é de fato bem estúpido querer multiplicar uma tabela por outra sem dar uma razão decente para isso, e hoje lhes apresento uma. Vamos criar a matriz estocástica do Banco Imobiliário Zona Leste. As regras para a matriz são: na primeira linha e segunda coluna, por exemplo, colocamos a probabilidade de, estando na primeira casa, cair na segunda casa. Como vocês sabem, essa probabilidade é ½ (tirar cara). A primeira linha dessa matriz será, portanto: 0, ½, ½, 0; ou seja, a chance é zero de ficar no mesmo lugar (você vai se mover), ½ de avançar uma casa (cara), ½ de avançar duas (coroa) e zero de avançar três. A matriz total será:

\[M=\left(\begin{matrix}0&\frac{1}{2}&\frac{1}{2}&0\\ 0&0&\frac{1}{2}&\frac{1}{2}\\ \frac{1}{2}&0&0&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}&0&0\end{matrix}\right)\]

E ela vai nos ajudar a fazer todo o resto. A utilidade de escrevê-la, além de ficar claro e bonitinho, é a seguinte: ela representa na linha $i$ e coluna $j$ as probabilidades de, estando na casa número $i$, ir à casa número $j$ em uma jogada. Se eu quiser a probabilidade de, estando na linha $i$, ir à coluna $j$ em duas jogadas, basta multiplicar a matriz $M$ por ela mesma! Aos que estão enferrujados em multiplicação de matrizes, eis a resposta:

\[{}\left(\begin{matrix}0&\frac{1}{2}&\frac{1}{2}&0\\ 0&0&\frac{1}{2}&\frac{1}{2}\\ \frac{1}{2}&0&0&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}&0&0\end{matrix}\right).\left(\begin{matrix}0&\frac{1}{2}&\frac{1}{2}&0\\ 0&0&\frac{1}{2}&\frac{1}{2}\\ \frac{1}{2}&0&0&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}&0&0\end{matrix}\right)=\left(\begin{matrix}\frac{1}{4}&0&\frac{1}{4}&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{4}&0&\frac{1}{4}\\ \frac{1}{4}&\frac{1}{2}&\frac{1}{4}&0\\ 0&\frac{1}{4}&\frac{1}{2}&\frac{1}{4}\end{matrix}\right){}\]

Ou seja, a chance de, estando na primeira casa, voltar a ela depois de duas jogadas é 1⁄4, a chance de estar na terceira casa depois de duas jogadas também é 1⁄4 e a chance de estar na quarta casa é ½. Mas o problema não é saber as chances de 2, 3, 10 ou 100 jogadas, queremos saber qual é a mais provável de cairmos em todo o decorrer da partida, o que é um problema diferente, mas que pode ser resolvido com essa matriz. Basta multiplicar essa matriz por ela mesma um número alto, bem alto de vezes, torcer para que ela comece a convergir para uma matriz razoável e dizer que essas serão as probabilidades em “tempo infinito”, ou seja, as chances de se estar naquelas casas depois de ter jogado muitas vezes.

Note, dizer que em um número alto de jogadas eu estarei mais provavelmente na casa X e dizer que terei passado várias vezes por X são afirmações bem diferentes, mas arrisco dizer que representam a mesma coisa, e o nome dessa afirmação é hipótese ergódica. Esse post não tem a menor pretensão de avançar nessas águas, que esse nome fique sendo, por enquanto, apenas um nome bonito para uma teoria.

Mas se elevar uma matriz ao quadrado é difícil, como elevar uma matriz a um número muito grande? Matematicamente falando, vamos elevar $M$ a $n$, o número de jogadas, e depois tomar o limite para $n\to\infty$, ou seja, vamos dizer que $n$ é um número muito, muito grande; o que, para Banco Imobiliário, consiste em uma excelente aproximação.

Parte geek do post, evite se não reconhecer a palavra “autovalor”. A parte rookie continua em seguida.

Os que já fizeram seu curso de álgebra linear conhecem a dica, vamos atrás dos autovalores dessa matriz e elevar esses caras a $ n$, depois mandar $ n$ para infinito e ver no que vai dar. Isso porque, felizmente, se escrevemos uma matriz como $M=UDU^{-1}$, onde $D$ é uma matriz diagonal, elevar $M$ a $n$ é escrever $ UDU^{-1}UDU^{-1}\ldots UDU^{-1}$ um número $ n$ de vezes, notando que os $ U^{-1}U$ do meio se cancelam, isso é o mesmo que $ UD^nU^{-1}$, e elevar uma matriz diagonal a uma potência é simplesmente elevar seus elementos a essa potência.

Posso me colocar várias perguntas como: “e se algum autovalor for maior que 1? A matriz vai explodir!” ou “E se todos forem menores que 1? A matriz vai para zero!” ou ainda: “E se algum for negativo? Como você eleva isso a infinito?!”; mas todas elas são sanadas quando invoco um corolário do poderoso teorema de Perron-Frobenius:

Teorema (de Perron-Frobenius): Entre outras coisas (esse teorema é bem poderoso), uma matriz estocástica como a do banco imobiliário possui o autovalor 1, único (não degenerado), e não há autovalores que, em módulo, sejam maiores que ele. O autovetor associado ao autovalor 1 possui todos os seus componentes de mesmo sinal. Em particular para matrizes como as do Banco Imobiliário, esse valor próprio 1 é o maior de todos os autovalores em módulo.

Eu poderia discutir bastante a razão desses resultados, já que Perron-Frobenius é um canivete suíço, adaptando-se a vários tipos de matrizes não-negativas diferentes. No caso da do Banco Imobiliário temos o fato importante de ser perfeitamente possível estar na casa $ i$ e voltar a ela mesma após um número $ m$ suficientemente grande de jogadas, e também ser possível voltar após $ m+1$ a essa mesma casa. Essa propriedade garante que 1 será o único autovalor de $ M$ no círculo unitário.

Esse corolário não deve surpreender ninguém, pois, se uma matriz estocástica vezes outra matriz estocástica continua uma matriz estocástica (eu teria que demonstrar isso, mas acredite em mim, é verdade), $ M^n$ deve também ser estocástica, então não pode ter autovalores maiores que 1 (que explodiriam se elevados a $ n\to\infty$), também não poderia ter apenas autovalores menores que 1, a matriz toda iria a zero quando elevada a $ n\to\infty$, não sobra tantas alternativas além do resultado de Perron-Frobenius. O que ele nos garante de interessante é a unicidade desse autovalor 1 e o sinal do autovetor associado.

E se você elevar todos os demais autovalores a $ n\to\infty$, eles logo logo vão para zero. Sobra o 1. Reconstruindo a matriz multiplicando por $ U$ e $ U^{-1}$, teremos uma surpresa, $ M^n$ com $ n\to\infty$ possui todas as linhas iguais, cujos componentes são os elementos do autovetor associado a 1. Essa surpresa é consequência da teoria ergódica, mas isso fica para outro post Dessa forma, o que queremos é esse autovetor associado ao autovalor 1.

Fim da parte geek.

O método descrito acima, se aplicado a nosso Banco Imobiliário Zona Leste, nos dará que a probabilidade de cair em todas as casas é a mesma, o que é esperado. Somos tentados a achar que no jogo do Banco Imobiliário ocorre o mesmo, mas esquecemos de elementos fundamentais da dinâmica do jogo, em particular da prisão, que muda tudo. Para explicar o efeito da prisão nas probabilidades das casas, introduzo um novo jogo, o Banco Imobiliário Zona Leste Deluxe:

Jogaremos usando um dado de seis faces. Nesse novo jogo, a matriz não será tão bonita quanto a anterior. A casa “Vá para a prisão” leva diretamente à prisão, quebrando a simetria do jogo e beneficiando as casas logo após a prisão, prejudicando aquelas que vêm antes. A matriz completa desse jogo será:

\[M=\left(\begin{matrix}0&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&0\\ 0&0&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}\\ \frac{1}{6}&0&0&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}\\ \frac{1}{6}&\frac{1}{6}&0&0&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}\\ \frac{1}{6}&\frac{1}{6}&\frac{1}{6}&0&0&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}\\ \frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&0&0&\frac{1}{6}&\frac{1}{6}\\ 0&0&1&0&0&0&0&0\\ \frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&0&0\end{matrix}\right)\]

Aquela bela simetria da outra matriz já não mais existe, a prisão é a culpada, note a penúltima linha (representando a casa “Vá para a prisão”). Analisando quais serão as probabilidades de se cair em cada uma das casas após um grande número de jogadas usando a técnica da parte geek, ou seja, multiplicando a matriz por ela mesma muitas vezes, teremos:

O que é bem diferente de uma probabilidade uniforme, como no jogo anterior.

Apliquemos tudo isso ao verdadeiro Banco Imobiliário. Seu tabuleiro é mais completo, ele é jogado com dois dados e andamos a soma dos valores tirados, possui casas de sorte-ou-revés, diversas cores e muitas propriedades. Seu tabuleiro, a quem não se lembra, é:

Não vou escrever sua matriz estocástica, não quero cuspir uma tabela de 40 linhas e 40 colunas nesse blog, mas acreditem, fiz as contas. A probabilidade de se encontrar em cada uma das casas é:

Levei também em conta a chance de 1/18 de se encontrar uma carta de ida à prisão nos espaços de sorte-ou-revés, foi o ajuste mais fino que fiz no modelo, para obter esses resultados. Ainda, ele não afeta em grande coisa a análise, pois as casas de sorte-ou-revés estão bem distribuídas no tabuleiro, apenas acentuam o efeito da prisão.

Notem que as casas rosa não são apenas as mais baratas e de pior rentabilidade, são também aquelas, juntamente com as azuis escuras, mais difíceis de atingir no tabuleiro. Interlagos e Morumbi, as tão desejadas laranjas, formam a dupla mais provável de casas para se atingir: são aquelas mais prováveis de encontrar após sair da prisão e, sendo a prisão a casa de longe mais provável, elas herdam um pouco dessa probabilidade.

Não jogo Banco Imobiliário há muito, entendo um pouco a razão. Podemos imaginar razões para a casa mais cara ser a mais provável, ou outras sutilezas descobertas na análise, mas isso é facilmente refutado pelo fato de países diferentes escolherem distribuições diferentes de valores de casa pelo tabuleiro; no jogo francês, a casa mais cara é a menos provável, substituindo o Jardim Paulista de nossa edição. Percebemos, por isso, que não é um jogo feito com tanto cuidado assim. Contudo, talvez se quando eu jogava soubesse um pouco mais sobre matrizes, mais sobre Frobenius, tivesse mais sorte no dado, talvez assim eu tivesse gostado, jogado, ganhado, ou, quem sabe, até mesmo terminado uma partida de Banco Imobiliário.

12 respostas

Coleção completa

Geek

Quando era criança, fui atingido pela mania dos tazos da Elma Chips como todos os meus colegas. Abria o salgadinho antes mesmo de chegar à aula, longe ainda do recreio, e recolhia o precioso prêmio do pacote: um disco plástico que servia de moeda de aposta e demonstração de habilidade no intervalo. Eu não era muito bom nisso, e não tinha tantos amigos, então minha principal fonte de Tazos eram o fandangos.

Via colegas com tubos repletos de tazos, coleções completas, era invadido por essa inveja e, talvez mais, por uma pergunta séria: como aquilo era possível? Eu colecionava havia meses e não chegara perto da metade da coleção, possuía muitos repetidos e aquele do Papa-Léguas era mais difícil de encontrar que filhote de pomba. Não imaginava como aquilo era possível, culpava os pais do garoto sortudo, deviam ter comprado caminhões de baconzitos, e, no fundo, queria saber: de quantos fandangos eu precisaria para completar minha coleção?

Essa pergunta está mal-feita, vamos melhorá-la. Mais interessante seria perguntar: qual o número médio, o valor esperado, de salgadinhos que preciso comprar para completar minha coleção? Em outras palavras, a partir de qual número de fandangos é mais provável que eu já tenha a coleção completa que o contrário? E, como pergunta bônus, quão improvável se torna, a partir desse número, não obter os preciosos tazos?

Havia tazos mais raros, é verdade, mas a pergunta já está bem difícil, então tomo como hipótese que a chance de tirar qualquer um dos tazos é a mesma. E para continuar, precisamos primeiro saber quantos são eles, e eis a coleção toda:

Se você está interessado na resposta, mas não conhece tanto de probabilidade, o que segue não será tão interessante (vou fazer as contas, é o que faço da vida, não consigo evitar). Mas você pode pular para o final do post e ver as conclusões sem culpa, se confiar em mim. Se, no entanto, você entende de probabilidade, jamais confie em mim. Suponha que eu já tenha $ k$ tazos diferentes, sendo $ n$ possíveis, a chance de eu tirar um repetido é $ \frac{k}{n}$. Assim, a probabilidade de eu precisar de exatamente $ s$ salgadinhos para tirar um diferente é $ \left(\frac{k}{n}\right)^{s-1} \left(1-\frac{k}{n}\right)$, que é uma parte a chance de eu tirar $ s-1$ repetidos e outra parte, no $ s$-ésimo salgadinho, tirar um diferente. Essa é $ P(s)$, a chance de eu precisar de $ s$ fandangos para tirar meu tazo diferente. Para calcular o valor esperado de salgadinhos até o próximo tazo diferente, ou seja, de $ s$, basta tomar:

\[ \sum_{s\geq 0}P(s).s=\sum_{s\geq 0}\left(\frac{k}{n}\right)^{s-1}\left(1-\frac{k}{n}\right).s=\frac{1}{1-\frac{k}{n}}\]

Essa última passagem fiz na malandragem, vale a pena explicar. Vou chamar $ \frac{k}{n}$ de $ x$ porque digitar essas coisas no WordPress cansa. Vou aplicar a distributiva, manobrar os índices e converter tudo em uma progressão geométrica de soma bem fácil:

\[\sum_{s\geq 0}x^{s-1}\left(1-x)\right).s=\sum_{s\geq 0}x^{s-1}s-\sum_{s\geq 1}x^s.s=\sum_{s\geq 0}x^s(s+1)-\sum_{s\geq 0}x^s.s=\sum_{s\geq 0}x^s=\frac{1}{1-x}\]

Então o número esperado de salgadinhos que devo comprar é a soma dos salgadinhos esperados para cada tazo que vou tirando, ou seja:

\[ \sum_{k=0}^{n-1}\frac{1}{1-\frac{k}{n}}=\frac{n}{n}+\frac{n}{n-1}+\ldots+\frac{n}{2}+\frac{n}{1}\]

Sem magia até agora, eu apenas expandi a série. Eu poderia calcular exatamente esse valor para $ n=80$, mas gosto de resultados mais gerais, e noto que essa soma é $ n$ vezes a série harmônica. Ela diverge, e não é surpreendente que eu precise de infinitos fandangos para tirar infinitos tazos, mas felizmente conhecemos razoavelmente bem o comportamento dessa série. O número esperado de salgadinhos necessários para completar uma coleção de $ n$ tazos é, portanto, $ nH_n$, onde $ H_n$ é o n-ésimo número harmônico. Para $ n$ grande, podemos usar a aproximação $ H_n\approx \log n+\gamma$, onde $ \gamma$ é a constante de Euler-Mascheroni (aproximadamente 0,5772).

Chegamos ao valor $ 80*(\log(80)+\gamma)=396,74$, certamente aproximado. Esse é o número médio de vezes que crianças completam suas coleções. Temos a média, a próxima pergunta é: quão provável é estar longe da média? Ao invés de tentar calcular com manobras intrincadas as flutuações desse número em torno da média, tomarei, a princípio, o exemplo de cinco crianças: Aline, Bruno, Carlos, Daphny e Eduardo. Eles começam suas coleções juntos e têm poucos amigos, logo, contam apenas com os salgadinhos para obter os preciosos discos. Eis uma simulação que fiz do resultado da coleção dessas cinco crianças:

Notamos algumas coisas interessantes. Primeiro, teremos que gastar aproximadamente metade dos salgadinhos totais necessários apenas para conseguir os dez últimos tazos; a matemática é cruel com coleções quase completas. Segundo, o valor necessário para completar é muito diferente nos cinco casos, isso exige um estudo mais sério.

Para tal, calibramos o computador para simular a coleção de tazos, ou o álbum de figurinhas (o problema é o mesmo) de 20.000 crianças. Fiz um histograma com a quantidade de salgadinhos necessária para completar toda a coleção e a porcentagem das crianças simuladas que precisaram daquela quantidade de salgadinhos para obterem o último tazo.

Notamos a larga variância dessa distribuição: haverá um grande número de crianças sortudas e um grande número de azaradas! Confirmamos o valor esperado, 396 parece de fato uma boa média dessa distribuição, e confirmamos o quão sórdido é o raciocínio da Elma Chips: algumas crianças precisariam de 900 salgadinhos para terem a coleção completa!

Contudo, esse modelo não representa bem a realidade, talvez apenas a minha, mas a maior parte das crianças tinha como maior objetivo as trocas de tazos, as disputas, completar a coleção contando com o salgadinho dos outros. Eu mesmo consegui dois amigos para fazer uma sociedade, ainda que cada um quisesse, para si, uma coleção completa. E esse será meu modelo de trocas: os amigos são amigos perfeitos, todo tazo repetido é compartilhado e o objetivo maior é, para $ y$ amigos, formar $ y$ coleções completas.

De forma não surpreendente, o número de fandangos que cada criança deve comprar reduz drasticamente com as trocas. Se ele antes precisava gastar quase um ano de lanches de salgadinho para encontrar os dez últimos, esses famigerados dez podem ter sido encontrados por algum colega que já até o tirou uma vez. Simulei o resultado com grupos de 1, 5, 10 e 30 crianças, sendo os resultados no histograma abaixo:

Esses valores são quantos fandangos cada um precisará comprar, ou seja, no grupo de dez, se dez amigos precisaram de 2000 fandangos para fechar a conta, contabilizo 200 para cada criança. Os valores médios de salgadinhos individuais obtidos para 1, 5, 10 e 30 são, respectivamente e aproximadamente, 398, 194, 154 e 120. Fiquei curioso para estudar a convergência dessa série, se vai para algum lugar (certamente converge, sendo decrescente e limitada em 80) e se esse lugar é 80, uma utopia em que todas as crianças do país montam suas coleções juntas; mas esse post já está longo e tanto salgadinho não deve fazer bem a esses meninos.

Por fim, noto que a amizade é o melhor investimento, você pode, em poucos meses de lanche, completar sua coleção de tazos ou figurinhas se encontrar, em uma sala de aula, trinta amigos perfeitos. A probabilidade desse fato, no entanto, mesmo em um modelo bem otimista, é extremamente baixa.

2 respostas

Aniversários

Rookie

Hoje é meu aniversário, celebro vinte e quatro anos de vida. E essa data, além de me fazer sentir especial, costuma me lembrar de um problema fascinante de combinatória, que levou a um igualmente interessante estudo econômico. Como não achei referência ao estudo, nem lembro onde o li, repeti-o eu mesmo, na medida do possível. O problema é conhecido como paradoxo do aniversário, que de paradoxal não tem nada.

A pergunta é: quantas pessoas eu preciso colocar em uma sala para que a chance de haver naquela sala pessoas com o aniversário repetido seja maior que a chance de não haver pessoas com o aniversário repetido? Formulado de outra maneira, eu tenho $N$ pessoas em uma sala e uma probabilidade $P(N)$ de que essas pessoas possuam aniversário repetidos, qual o primeiro valor de $N$ para o qual $P(N)>0,5$?

E a resposta é um número surpreendentemente baixo: 23. A partir desse valor de pessoas, é mais provável encontrar pessoas com aniversários repetidos que não encontrar, a probabilidade de que duas pessoas tenham nascido no mesmo dia do ano passa a 50,7% para esse valor de $N$. A razão do número ser pequeno é o grande crescimento da função fatorial, usada para calcular o número de combinações possíveis para a comparação de cada par de pessoas. Ou seja, apesar de haver muitos dias no ano, o número de comparações possíveis entre o aniversário de 23 pessoas é suficientemente grande para tornar essa probabilidade maior que 50%.

Interessados nesse resultado, podemos testar os aniversários de partidas de futebol. Sendo 11 para cada lado e o juiz, teremos 23 pessoas a cada partida, e podemos comparar um número grande de partidas para perceber que há mais partidas com aniversários repetidos que partidas sem aniversários repetidos.

No entanto, o resultado não será o que esperamos. De fato, há muitas partidas com aniversários repetidos, mas um número muito maior que o esperado! As partidas com aniversários repetidos ocorrem em número muito maior que as que não possuem aniversários em comum, quando a diferença não deveria estar muito longe de 51% contra 49%. Esse fato foi-me apresentado há algum tempo, foi-me até dito que um estudo foi feito, jamais achei o estudo, fi-lo eu mesmo com a ajuda da Wikipédia e sua excelente página da escalação de cada seleção de futebol.

Pus-me a anotar os meses de nascimento dos jogadores de futebol das seguintes seleções: Brasil, Paraguai, Chile e Argentina. Tomei a escalação mais atual possível, para não haver privilégio de uma época ou outra. A razão de pegar apenas países do hemisfério sul ficará clara com os resultados.

Enquanto o Paraguai não apresenta uma distribuição de nascimento de seus jogadores ao decorrer do ano que chame a atenção, Brasil, Chile e Argentina impressionaram-me e comprovaram, em termos nada rigorosos, a teoria que eu havia ouvido a respeito do estudo. Organizei um histograma em três camadas, as barras menores são os nascimentos no mês, as intermediárias representam nascimentos em um trimestre e as grandes são os nascimentos no semestre. O resultado do Paraguai, analisados 83 jogares, foi:

Nada impressionante até aqui, os aniversários parecem razoavelmente bem distribuídos em todos os níveis e não consigo perceber uma tendência evidente. No entanto, a distribuição do Brasil já começa a apresentar um fenômeno interessante:

Temos na seleção brasileira, analisados os 69 últimos convocados de Mano Menezes, uma concentração clara de nascimentos no primeiro semestre, em especial uma forte ausência de nascidos no último trimestre do ano. Claro, isso pode ser uma improbabilidade realizada, não um indício de variável escondida. Se analisarmos com cuidado, podemos calcular a probabilidade de, jogando aniversários aleatoriamente no ano, ter essa diferença entre o primeiro e o segundo semestre; é improvável, mas nem de longe impossível.

No entanto, os resultados do Chile, analisados 77 jogadores, revelaram-se:

E essa diferença entre primeiro e segundo semestre já não pode mais ser explicada como uma anomalia estatística, há algo estranho nesse país que faz jogadores de futebol nascerem no começo do ano e não no final. Para confirmar a teoria, podemos avançar no estudo da seleção Argentina, analisando 92 jogadores:

Esse gráfico não pode, de maneira alguma, ser justificado como coincidência. A albiceleste possui o dobro de jogadores nascidos no primeiro semestre em relação ao segundo semestre. Entrementes, notamos que em todas as seleções dezembro é sistematicamente o pior mês, ou o segundo pior, no caso do Chile.

Podemos nos divertir calculando a probabilidade de obter uma configuração como a da Argentina se os aniversários fossem distribuídos de maneira uniforme no ano. Temos 92 jogadores e queremos saber a chance de, distribuindo aleatoriamente no ano, ter uma diferença de 30 nascimentos entre os dois semestres, sendo o primeiro semestre o favorecido. Calculando com cuidado, essa probabilidade não passa do valor 0,08%, extremamente baixa, ela precisa de uma explicação.

Antes que os astrólogos saiam em defesa de alguma correlação entre estrelas e seres humanos, comento a conclusão a que chegaram os estatísticos. Essa predominância de nascimentos em um semestre não ocorre em países europeus, curiosamente, analisei França e Inglaterra e os resultados não são nada impressionantes. Esses três países do sul, Brasil, Argentina e Chile, apresentam sistematicamente jogadores nascidos em um semestre, e a razão disso, muito provavelmente, é o ano letivo.

No mesmo argumento que usou Malcolm Gladwell em seu livro Outliers para explicar jogadores de hóquei, nesses países, as escolas de futebol organizam os alunos de acordo com o ano letivo, e os jogadores profissionais enfrentam peneiras desde cedo para seguir na carreira. Os nascidos no começo do ano são, por isso, os mais velhos de suas turmas e, ao enfrentam peneiras desde crianças, são também os mais fortes e mais rápidos. Os nascidos no primeiro trimestre são quase um ano mais velhos que os nascidos no último, e são selecionados em uma idade em que um ano é muito para o desenvolvimento corporal. Esse resultado é ausente nos times europeus porque as escolas de futebol não seguem um ano específico, algumas tomam o escolar como base e outras o ano de nascimento, não havendo consenso, há equilíbrio na distribuição.

Falta, claro, explicar o caso do Paraguai. Tendo em vista os outros países, o mais natural é supor, ou que o Paraguai é a anomalia estatística, ou que o sistema de escola de futebol e peneira desde muito cedo não é tão rigoroso no Paraguai.

Tudo o que eu acabo de fazer, aviso, consiste em estatística de péssima qualidade. Eu precisaria tomar vergonha na cara, analisar mais jogadores de mais times, informar-me sobre o sistema de avaliação do Paraguai e não me ater a essa tese com muito afinco, ela pode muito bem estar furada. Contudo, os 0,08% chamam a atenção, e confirmam que o estudo do paradoxo do aniversário não pode ser realizado com jogadores de futebol.

Claro que a hipótese feita, a distribuição igual de nascimentos ao redor do ano pela população normal, precisa ser justificada. Redireciono-os ao trabalho desse site, enquanto aponto ao curioso fato do grande número de nascimentos em setembro-agosto, provavelmente resultado das férias de natal, quando a chance de se estar em casa é alta e a programação da televisão cai de qualidade vertiginosamente.

Se o futebol sul-americano já apresenta esse fenômeno, podemos encontrá-lo de forma ainda mais acentuada em esportes cuja dependência da disposição física (e, logo, da idade) seja maior, o hóquei é um bom exemplo. Um grande estudo nesse aspecto foi realizado no Canadá em 1988 e os resultados do estudo são impressionantes, o mês de nascimento parece ter implicação direta no sucesso do jogador. Atualmente, parece que as ligas americanas e canadenses adaptaram um calendário diferente, mais próximo daquele europeu de futebol, e a diferença não é mais gritante.

E esses gráficos nos inspiram a questionar o quanto do sucesso de alguém em uma carreira é fruto de sucesso inicial, de ter se dado bem no começo, gostado, continuado, se esforçado e se dado ainda melhor, um círculo vicioso positivo vindo apenas do fato de ter sido bem sucedido no começo. Extrapolando, podemos nos perguntar se fazemos o que fazemos pelo sucesso inicial, e me pergunto quanto da matemática que faço não vem de uma primeira nota alta na matéria. As coisas talvez tivessem sido diferentes se eu tivesse errado mais questões, se minha professora fosse uma carrasca, se a ponta de meu lápis tivesse quebrado naquela primeira prova ou, quem sabe, se eu tivesse nascido em junho.

19 respostas