Minha namorada está buscando um apartamento para alugar em Paris começando no mês de novembro, e a busca tem sido uma tragédia em diversos atos. Cubículos pequenos, muita competição, preços altos e até imobiliárias que mais parecem esquema de pirâmide que um estabelecimento sério têm acompanhado a jornada dessa física teórica nas últimas duas semanas. Quanto aos preços, ao menos há um fator positivo, uma lei recente baixada inspirada na solução que Berlim tenta implementar para resolver seu problema de aluguéis: um teto de preço baseado no valor médio das redondezas.
A lei diz que o valor de um aluguel não pode ser superior à média do bairro de uma diferença maior que 10%. Ou seja, se a média do bairro é 22 euros o metro quadrado, um aluguel não pode ser mais alto que 24,2 euros o metro quadrado. Simples assim. Essa é uma ideia bem divertida, que me fez considerar a seguinte questão: o problema da Berlim gananciosa.
Nessa nova Berlim, a lei é um pouco mais rígida. Uma pessoa não pode impor um aluguel maior que a média de seus vizinhos cuja diferença entre a média e o aluguel seja maior que 10%. A pergunta é: é possível que exista uma cidade com essa lei em que todas as pessoas cobram o maior aluguel possível pela lei? Ou seja, obrigando as pessoas a cobrarem exatamente 110% da média de seus vizinhos, é possível haver uma cidade em que todas as pessoas conseguem cobrar essa quantia?
Para bem definir o problema, vamos estabelecer hipóteses fundamentadas na realidade. A primeira: minha cidade é unidimensional, parecida com Cuernavaca, porque quero uma noção de vizinhança bem definida e porque D=1 é meu número favorito de dimensões. Segunda: casas na periferia não têm esperança de ganhar dinheiro no aluguel em relação aos vizinhos e possuem preço fixo. Isso vem do fato, inspirado em minha experiência parisiense, de que morar longe do centro só é bom se for na direção de Versailles, e olhe lá. Isso fixa as condições de contorno do problema. Dado um preço fixo nas casas da periferia, é possível que o resto da cidade cobre um aluguel superior em $\alpha$ porcento à média de seus vizinhos?
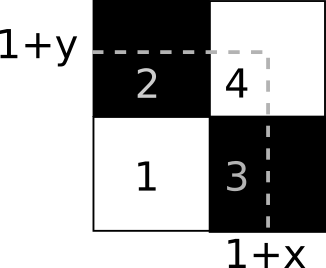
A resposta, e já mando com spoilers, é: depende do $\alpha$. Há valores em que isso é possível, mas existe um limite para a extorsão de seus inquilinos se você precisa respeitar a regra dos $\alpha$ porcento. Para entender o que acontece, vamos começar com o caso de uma cidade pequena, a cidade de Berlim de três habitantes, chamada $B_3$. Vejamos a cara dessa cidade.
 A regra geral das casas de Berlim gananciosa é:
A regra geral das casas de Berlim gananciosa é:
\[ x_n = \frac{(1+\alpha)}{2}(x_{n+1}+x_{n-1}).\]
Seja $(1+\alpha)/2=\lambda$, para simplificar nossa vida. A única exigência da primeira cidade de Berlim que vamos estudar, $B_3$, é que $x_2=\lambda (1+1)=2\lambda$, então o valor de $\lambda$ pode ser qualquer coisa, não há limites para a ganância de $B_3$
O caso de $B_4$, no entanto, é diferente. Vejamos como é essa cidade:
 Neste caso, os valores de $x_2$ e $x_3$ serão fixos pelo sistema
Neste caso, os valores de $x_2$ e $x_3$ serão fixos pelo sistema
\[ \begin{cases} x_2=\lambda(1+x_3) \\ x_3 = \lambda(1+x_2) \end{cases} .\]
Vocês sabem que eu gosto de matrizes, então vamos colocar isso em notação de gente grande. Os aluguéis de $B_4$ serão definidos pelo sistema
\[ \left(\begin{matrix} 1 & -\lambda \\ -\lambda & 1 \end{matrix}\right)\left(\begin{matrix} x_2 \\ x_3 \end{matrix}\right) = \left(\begin{matrix} \lambda \\ \lambda \end{matrix}\right).\]
Esse é um sistema linear bem bonito, mas vocês devem se lembrar das aulas do ensino que diziam, com razão, que a vida fica mais cinza, o mundo perde a cor e você perde a vontade de cantar uma bela canção quando o determinante da matriz que define o sistema linear se anula. Quando isso acontece, não há mais solução possível para o sistema. E note que o determinante que nossa querida matriz é
\[ \det \left(\begin{matrix} 1 & -\lambda \\ -\lambda & 1 \end{matrix}\right) = 1-\lambda^2. \]
Ou seja, algo muito errado acontece quando $\lambda=1$, que acontece no mesmo momento em que $\alpha=1$. Não apenas o sistema não tem solução, não há mais valor de alguel possível para satisfazer tanta ganância, mas se você tentar impor um $\lambda$ mais alto que um, não encontrará a solução que deseja. Se $\lambda > 1$, a solução do sistema apresentará valores negativos de $x_2$ e $x_3$, e acho que é seguro acrescentar como hipótese baseada na realidade que preços de aluguel devem ser positivos.
Assim, percebemos que com quatro casas o valor máximo que a lei pode impor para a extorsão dos inquilinos é de $\lambda=1$, o que equivale a $\alpha=1$, ou o máximo que podemos impor é que uma casa cobre o dobro da média dos vizinhos. Vejamos o que acontece quando a cidade é maior, visitemos $B_5$.
 Nesse caso o sistema linear que define os valores de $x_2$, $x_3$ e $x_4$ será
Nesse caso o sistema linear que define os valores de $x_2$, $x_3$ e $x_4$ será
\[ \left(\begin{matrix} 1 & -\lambda & 0 \\ -\lambda & 1 & -\lambda \\ 0 & -\lambda & 1 \end{matrix}\right)\left(\begin{matrix} x_2 \\ x_3 \\ x_4 \end{matrix}\right) = \left(\begin{matrix} \lambda \\ 0 \\ \lambda \end{matrix}\right). \]
Vamos chamar a matriz que define esse sistema 3 x 3 de $A_3$. A partir de agora, a matriz que define o sistema $n \times n$ será $A_n$. O determinante dela pode ser calculado com aquela técnica que você aprendeu no segundo colegial e errava toda vez que tentava fazer de cabeça sem usar aquela técnica das duas colunas fantasmas que você copia ao lado da última.
\[ \det A_3 =1-2\lambda^2 \]
E o determinante se anula no valor $\lambda = \sqrt{2}/2$, o que equivale ao valor de $\alpha=\sqrt{2}-1\approx 0.71$, que é menor que um. É fácil perceber a tendência desse problema: quanto maior a cidade, menor é a taxa de ganho extra que podemos cobrar e ainda exigir que todos cobrem mais aluguel que seus vizinhos. O valor de $\alpha$ diminui com o número de casas $N$ da cidade! Mas… diminui como?
E aqui vou descrever como foi meu processo para resolver esse problema. Eu queria achar a relação entre o $\alpha$ máximo e $N$, o tamanho da cidade. Eu sabia que $\alpha$ seria decrescente em $N$, mas não sabia como. Seria $\alpha$ proporcional a $1/N$? Ou a $1/N^2$? Ou talvez uma exponencial negativa de $N$? A exponencial eu podia ignorar, vi matrizes vezes demais no olhos e sei que esse tipo de problema terá uma relação polinomial, mas não vou excluir a possibilidade. Para resolver esse problema, a primeira coisa que fiz foi pensar como físico, ou seja, trigger warning aos que gostam de um raciocínio matemático rigoroso. Vamos pegar uma cidade muito grande, grande o suficiente para ignorar as bordas, e vamos voltar à equação principal do modelo:
\[ x_n = \frac{(1+\alpha)}{2}(x_{n+1}+x_{n-1}).\]
E podemos jogar um pedaço para lá e outro para cá para obter uma outra forma dessa equação de recorrência:
\[ \alpha (x_{n+1}+x_{n-1}) = x_{n+1}+x_{n-1}-2x_n.\]
O termo à direita é um velho amigo nosso, é uma segunda derivada discreta do aluguel. Nós brincamos com algo parecido em um dos primeiros posts desse blog, sobre a interpretação física do Laplaciano, e chegou a hora de usá-la. Eu tenho que dividir esse termo da direita por um diferencial ao quadrado para obter uma derivada, e esse diferencial é o tamanho de meu grid na derivada discreta. Em termos do modelo, eu defino que a posição de cada casa é dada pela variável $l$ e a distância entre duas casas é dada por $\Delta l^2$. Dividindo ambos os lados da equação por $\Delta l$ eu obtenho:
\[ \frac{\alpha}{\Delta l^2}(x_{n+1}+x_{n-1}) = \frac{x_{n+1}+x_{n-1}-2x_n}{\Delta l^2}.\]
O lado direito dessa equação, quando a cidade é bem grande e as casas são bem próximas, converge para $\frac{d^2x}{dl^2}$, enquanto o termo da esquerda pode ser simplificado lembrando que a soma dos vizinhos é $\frac{2x_n}{(1+\alpha)}$. Isso tudo resulta na seguinte equação diferencial:
\[ \sigma.x(l) = \frac{d^2x}{dl^2}.\]
Sendo
\[ \sigma = \frac{2\alpha}{(1+\alpha)dl^2}.\]
Eu sei que esse diferencial no denominador é revoltante a seu espírito matemático, mas não é mais minha responsabilidade zelar por seu coração sensível. Esse $dl$ é a distância entre duas casas. Suponhamos que a cidade toda tenha tamanho 1, em unidades de tamanho de cidade, então a distância média entre duas casas é $dl=1/N$. Para que essa equação diferencial faça algum sentido, eu preciso que $\sigma$ não seja nem zero, nem infinito, então, como exigência, eu preciso que $\alpha$ diminua conforme $dl$ diminui, ou seja, preciso que:
\[ \sigma=\frac{2\alpha}{(1+\alpha)dl^2}\sim 1\Rightarrow\alpha\sim\frac{1}{N^2}\]
Sendo esse $\sim$ o símbolo oficial de “tem o mesmo comportamento assimptótico de”, mas costumamos ler como: “se comporta como”, “é mais ou menos parecido em algum limite que eu espero que você tenha entendido” ou “não exatamente, mas tipo quase lá”.
Então o valor máximo da extorsão deve decrescer com o quadrado do número de casas. O problema está razoavelmente resolvido, mas o algebrista dentro de mim grita por uma solução melhor que essa. Vamos ver como seria aquela matriz $A_n$ para uma cidade bem grande. Teremos algo da forma:
\[ A_n = \left(\begin{matrix} 1 & -\lambda & 0 & 0 & \cdots & 0 \\ -\lambda & 1 & -\lambda & 0 & \cdots & 0 \\ 0 & -\lambda & 1 & -\lambda & \cdots & 0\\ \vdots & \ddots & \ddots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & -\lambda & 1 \end{matrix}\right).\]
$A_n$ é uma matriz tridiagonal com diagonal repleta de 1’s e co-diagonais preenchidas por $-\lambda$. Eu não apenas quero o determinante dessa criatura, eu quero encontrar as raízes do determinante e, mais especificamente, a primeira raiz que seja maior que $\frac{1}{2}$. Eu sei que $\lambda=\frac{1}{2}$ equivale ao caso $\alpha=0$, onde todos aluguéis são iguais à média dos vizinhos e, pelas condições nas bordas, isso representaria o caso em que todos os aluguéis são iguais a 1. Valores de $\lambda$ menores que meio representariam alguém cobrar um aluguel menor que a média dos vizinhos e, por mais que esse seja o sonho de minha namorada, não serão considerados. A primeira raiz do determinante que é maior que meio equivale ao primeiro valor de $\lambda$ que torna o sistema impossível, valores acima disso tornam alguns aluguéis negativos e não me interessam. Eu quero saber como a primeira raiz do determinante acima de meio se aproxima de meio quando o tamanho da matriz aumenta, e isso não é um problema muito fácil.
O determinante de uma matriz tridiagonal tem fórmula, e nesse caso essa fórmula é:
\[ \det A_n=\det A_{n-1}-\lambda^2\det A_{n-2} .\]
Isso não me ajuda muito, aliás, quase me desespera. Isso significa que o determinante será um polinômio de grau cada vez mais alto em $\lambda$ e eu conheço minhas limitações, resolver um polinômio de grau maior que quatro exatamente quase nunca é possível e eu começo a perder a esperança quando escrevo os primeiros cinco casos desse polinômio, eles não parecem ter nenhum padrão reconhecível e minha busca parece vã. Eu vou atrás das raízes desses polinômios, e lá as coisas começam a ficar interessantes.
No caso de $A_2$, encontramos $\lambda=\pm 1$ como raízes. Para $A_3$, temos as raízes $\lambda=\pm\frac{\sqrt{2}}{2}$. O determinante $A_4$ ainda tem raízes, é um polinômio de grau 4 que pode ser reduzido a um polinômio de grau 2 (a origem dessa redução é a simetria do problema, a segunda casa, por simetria, deve ter o mesmo valor da penúltima, por exemplo). As raízes são $\lambda=\pm \frac{1\pm\sqrt{5}}{2}$, que, aliás, são a razão áurea e sua inversa.
Espera… 1, $\frac{\sqrt{2}}{2}$ e razão áurea… eu conheço esses valores. Eles são todos cossenos de alguém (ou quase)! Isso não pode ser coincidência. O determinante de $A_n$ é um polinômio cujas raízes possuem uma ligação com cossenos. E quando eu percebi isso, fechei os punhos e soprei por entre os dentes cerrados a palavra Chebyshev…
Eu e você nos lembramos da aula de Física-Matemática II, quando Domingos Marchetti mandou aquela lista de exercícios que pedia para provar propriedades dos polinômios de Chebyshev. Entre elas, o fato de que polinômios de Chebyshev possuem $\cos(\frac{k\pi}{n+1})$ como raízes. Se eu quero um polinômio com essas raízes, preciso torturar Chebyshev. E eu devia ter desconfiado, veja a relação de recorrência que gera esses polinômios. Seja $T_n(x)$ o polinômio de Chebyshev (de segundo tipo) de grau $n$, teremos:
\[ T_{n}(x) = 2xT_{n-1}(x)-T_{n-2}(x) \]
E me diz se isso não é muito parecido com minha relação de recorrência dos determinantes de $A_n$! O determinante de $A_n$ não é exatamente $T_n(x)$, mas eu consigo ligar os dois com algumas manobras. O post já está longo e vou escrever direto a relação, é fácil chegar nela operando a relação de recorrência. Teremos
\[ \det A_n=(2\lambda)^nT_n\left(\frac{1}{2\lambda}\right).\]
Ou seja, se queremos as raízes do determinante de $A_n$, basta tomar o inverso das raízes do polinômio de Chebyshev! Sabemos que essas raízes são $x_k=\cos(\frac{k\pi}{n+1})$. Assim, as raízes de nosso determinante tridiagonal são dadas por:
\[ \lambda_k=\frac{1}{2\cos\left(\frac{k\pi}{n+1}\right)}\]
Sem surpresas, esses valores coincidem exatamente com 1, $\frac{\sqrt{2}}{2}$ e razão áurea. Queremos a primeira raiz acima de meio, ela é dada quando calculamos o valor $k=1$. Dessa forma, o maior valor possível da Berlim gananciosa será
\[ \lambda_{\text{max}}=\frac{1}{2\cos\left(\frac{\pi}{n+1}\right)}\sim\frac{1}{2}+\frac{\pi^2}{4N^2},\]
onde expandi para grandes valores de $N$ para ver o comportamento assimptótico de uma cidade grande. Como $\lambda=\frac{1}{2}+\frac{\alpha}{2}$, confirmamos que, para que esse sistema tenha soluções positivas, existe um limite máximo no lucro dos proprietários que diminui conforme o tamanho da cidade aumenta, e é dado por:
\[ \alpha<\frac{\pi^2}{2N^2}\]
Confirmando o que nossa intuição física já sabia naquele cálculo sem rigor acima, a dependência ocorre com o inverso do quadrado do número de habitantes na cidade unidimensional.
E no caso da cidade bidimensional? Não consegui resolver a matriz dessa, não houve Chebyshev que salvasse, mas o cálculo não rigoroso, que deu certo uma vez, parece indicar uma dependência no inverso de $N$, considerando uma cidade quadrada cujas bordas contém $\sqrt{N}$ casas enfileiradas.
Eu imagino que esse problema tenha sido um pouco mais difícil que o problema médio que apresento aqui, mas é fascinante. Nunca antes eu tinha encontrado polinômios de Chebyshev in the wild, tampouco com uma motivação tão interessante. Vou guardar esse na manga, esperando algum dia algum aluno preguiçoso, como eu era, perguntar-me de que servem esses tais polinômios cujo nome eu tenho que dar ctrl-c ctrl-v para não errar.
E uma nota final: minha namorada encontrou um apartamento finalmente. Fica em uma cidade simpática ao sul de Paris, com acesso ao metrô, mas não tão perto, com alguns metros quadrados, mas não tantos. Foi difícil achar, então comemoramos; mas confesso que, se perguntasse um pouco pelos corredores do prédio, provavelmente ficaria estarrecido em descobrir que o $\alpha$ desse lugar não respeita nenhum majorante.
 é se um dos lados do retângulo for um dos lados da imagem.
é se um dos lados do retângulo for um dos lados da imagem.