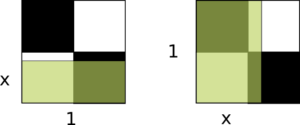Retângulos inteiros

Rookie

Quando eu era mais jovem, fiz uma prova oral de matemática dessas bem difíceis. Preparei-me durante quase dois anos apenas para essa prova, e o resultado foi bom, eu passei. Nela havia duas questões, uma de análise matemática e uma de álgebra linear, que eu nem me lembro direito ((Aos curiosos, a de análise era para provar a convergência de uma série de funções, dessas de provar que convergência de gente absolutamente contínua, e a de álgebra linear era para provar em que condições uma dada matriz 2×2 era diagonalizável, coisa fácil.)). Por sorte eu tinha estudado bem os temas que caíram e acabei, para minha surpresa, acabando a prova antes do tempo. Sem saber o que fazer, o examinador decidiu improvisar. Achando que seria interessante lançar uma “questão extra” para eu começar nos cinco minutos que faltavam, propôs-me um problema que me acompanhou durante esses últimos nove anos. Esse problema, e sua solução mais elegante que conheço, é o post de hoje. Seu enunciado é revoltantemente simples, e eu ainda lembro para que ponto da lousa ((Superior esquerdo.)) eu olhava quando o ouvi pela primeira vez:

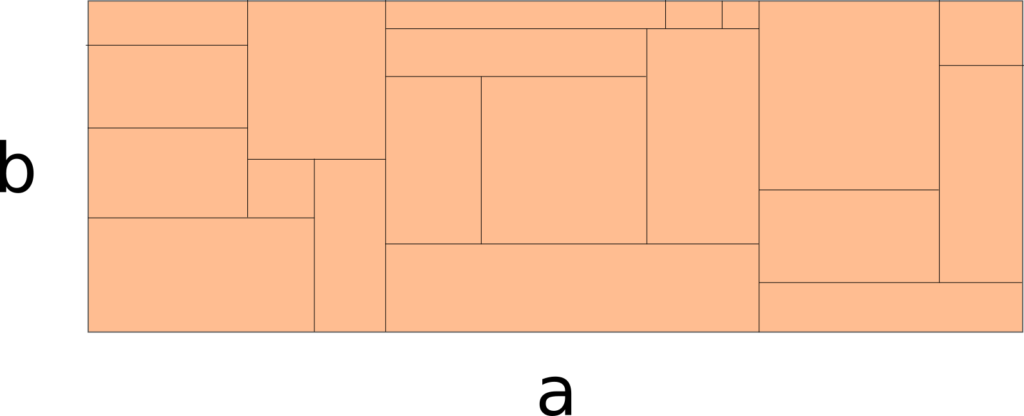
Imagine um grande retângulo composto de pequenos retângulos, como quarteirões de tamanhos variados que compõem um grande bairro retangular. Cada um dos pequenos retângulos tem um lado que é um número inteiro. Prove que o retângulo grande tem pelo menos um lado inteiro.

A solução padrão, aquela que eu mais encontro quando busco pelo problema na internet, envolve usar integrais complexas marotas que contam com o fato de um caminho em volta de cada retângulo ser equivalente a um caminho em volta do retângulo grande, pois os caminhos “internos” dos retângulos menores se compensam. Não vou entrar em detalhes porque, ainda que essa solução seja interessante, e provavelmente era a que o examinador queria, integrais complexas não fazem justiça à revoltante simplicidade desse resultado. Deve haver uma maneira mais intuitiva de provar isso, algo que esteja à altura da intuição que esse enunciado traz. Então vou apresentar a solução que encontrei cuja elegância mais se aproxima daquilo que eu esperava para esse problema, algo que tenha valido a pena esperar nove anos para ver.

Qual o problema desse enunciado? Ele é dado como uma verdade, mas ele não parece dever ser verdade. Eu consigo, em minha inocência e sem papel, imaginar que um retângulo poderia ser formado de pequenos retângulos com apenas um lado inteiro cada e, com um arranjo inteligente, ter dois lados que são frações, ou números irracionais. Mas o fato de o resultado ser verdade implica que eu terei um problema tentando fechar o retângulo. É um exercício fascinante que eu recomendo para entender de onde ver a intuição da solução que vou apresentar: tente compor um grande retângulo usando pequenos, desenhe livremente, apenas impondo que os retângulos internos tenham ao menos um lado inteiro. Invariavelmente você será confrontado com o problema de fechar o retângulo, e uma de duas opções será verdadeira: ou o retângulo que fecha o grande retângulo não terá um lado inteiro, ou o grande retângulo terá um lado inteiro.

A partir dessa intuição, vamos resolver esse problema. O melhor jeito de explorar essa questão de fechar o retângulo é de colocar todo o problema em um tabuleiro de xadrez 1/2 x 1/2. Algo mais ou menos assim:

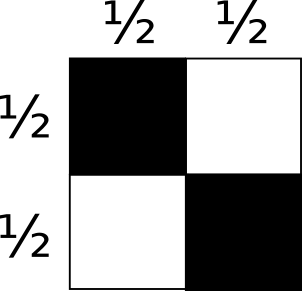E coloquemos também uma representação de nosso grande retângulo, com pequenos retângulos desenhados dentro apenas para referência (eu não desenhei isso em escala).

Nosso objetivo é provar que, se os retângulos internos têm todos ao menos um lado inteiro, então ou $a$ ou $b$ são inteiros. Vamos colocar isso no tabuleiro para ter algumas ideias.

O primeiro resultado importante que devemos listar aqui é o teorema fácil de ver: se um retângulo tem um lado inteiro, ele cobre uma área que é 50% branca e 50% preta. Ora, se um lado dele é um inteiro $p$, ele passa por $p$ quadrados pretos e $p$ quadrados brancos. Ainda que ele não comece exatamente na quina entre os quadrados, ele sempre atravessa a mesma quantidade de pretos e brancos naquele lado e, logo, pouco importa o quanto aumentamos ele do lado que não é inteiro, ele é obrigado a cobrir a mesma área de pretos e de brancos.

Cada um dos pequenos retângulos satisfaz o teorema acima, então cada um deles cobre a mesma área preta e branca. Visto que a área coberta pelo retângulo grande é a soma das áreas dos pequenos, o retângulo grande cobre a mesma quantidade de área preta e branca, pois cada uma de suas parcelas satisfaz essa propriedade.

É claro que isso não basta. Provei que todo retângulo de lado inteiro cobre pretos e brancos igualmente, mas preciso provar a volta, preciso provar que todo retângulo que cobre a mesma área de pretos e brancos tem ao menos um lado inteiro. Para isso, vamos provar por absurdo. Suponha que o retângulo grande não tem um lado inteiro. Então posso cortar o grande retângulo em quatro outros retângulos.

Este símbolo $\lfloor a \rfloor$ significa “parte inteira de $a$”, ou seja, arredondar o número $a$ para o baixo até encontrar um número inteiro. Por exemplo: $\lfloor 2.1\rfloor=2$. Minha ideia foi de quebrar o grande retângulo em um retângulo maior com os dois lados inteiros (o laranja), dois retângulos médios com pelo menos um lado inteiro (os vermelhos) e um pequeno retângulo com o que sobrou (o verde). Note que se o grande retângulo inicial não tem nenhum lado inteiro (nossa hipótese), o verde também não tem nenhum lado inteiro, porque os lados dele são “a parte que não é inteira” de $a$ e $b$. Se os lados do retângulo original fossem $2.5$ e $3.6$, os lados do retângulo verde seriam $0.5$ e $0.6$.

O retângulo laranja tem ao menos um lado inteiro (tem dois!), então cobre a mesma proporção de pretos e brancos. Os vermelhos também têm ao menos um lado inteiro, então também cobrem a mesma área de pretos e brancos. E agora vem o elemento chave, e aquele que usa o fato dos retângulos menores terem um lado inteiro: como eu sei que a soma desses quatro retângulos cobre a mesma área preta e branca, e como três deles também cobrem, o menor deles, o verde, deve obrigatoriamente cobrir a mesma proporção de área preta e branca.

Eu pareço apenas ter empurrado o problema com a barriga: antes queria provar que o grande retângulo cobrir a mesma área preta e branca implica ter lado inteiro, agora quero provar que um retângulo pequenino faz isso, parece trocar seis por meia dúzia. Mas há  uma diferença fundamental entre o retângulo verde e o grande retângulo: o retângulo verde começa em uma quina e é necessariamente menor que um quadrado 1×1.

E por que isso é importante? Tente desenhar um retângulo dentro de um quadrado 1×1 que cubra a mesma área de pretos e brancos. Sem muito esforço, você perceberá que só existem duas opções:

Ou ele é inteiro na horizontal e $x$ na vertical, ou ele é inteiro na vertical e cobre $x$ na horizontal. É impossível criar um retângulo de dimensões $x, y < 1$ começando na origem que cubra a mesma proporção de pretos e brancos!  Mas, por definição, o retângulo verde não possui nenhum lado inteiro, caímos em contradição! Como retângulo grande cobre a mesma área de pretos e brancos, o verde deve cobrir também, e a única maneira de isso acontecer, visto que ele está confinado no quadrado 1×1, é tendo um lado inteiro. Assim, o retângulo grande deve necessariamente ter um lado inteiro.

E o que eu fiz quando me apresentaram a pergunta, quando essa era minha questão final na prova oral? É evidente que entrei em pânico, ainda que tenha mantido a compostura. Meu cérebro correu toda a matemática que conhecia e eu não tinha a mais vaga ideia de nem por onde começar. Com cara de jogador de poker, esbocei um retângulo na lousa, escrevi dimensões $a$ e $b$ e fingi pensar um pouco. Porque o examinador percebeu meu pânico, ou por pura misericórdia divina, ele olhou o relógio e disse: “Ah, infelizmente temos apenas cinco minutos, acho que não vai dar para resolver.”. De fato, não dava em cinco minutos. Tivesse eu mais nove anos, quem sabe não apresentaria uma solução mais elegante.

2 respostas

A população brasileira

Rookie

A reforma da previdência é um assunto quente no momento. Um governo desestabilizado deve atacar uma importante reforma que leva em conta a situação política, econômica e demográfica brasileira. Não tenho competência para atacar a parte da economia, não acho que alguém tenha competência para entender qualquer coisa de política atualmente, então dedico um post às mudanças demográficas brasileiras dos últimos 17 anos, e futuros dois.

A evolução da população brasileira é fácil de achar no site do IBGE, mas não é fácil visualizar. Para isso, decidi afinar minhas habilidades em JavaScript e construir um gráfico interativo para facilitar a compreensão. Esse é o resultado:

View in percentage


Os dados usados são os reais até 2013 e projetados até 2020. Basta clicar em alguma barra, ou em alguma legenda, para visualizar uma faixa de idade com mais detalhe. Coloco aqui uma versão maior desse gráfico. Nessa página também disponibilizo o código e os dados; você pode fazer seu próprio gráfico interativo em casa, basta trocar os dados de entrada e ele deve, sem reclamar muito, montar-se sozinho.

O post de hoje é sem análise, o gráfico deve falar por si.

Deixe um comentário

A melhor forma de eleição

Rookie

O governo Temer não anda bem. Atingimos o dígito único em matéria de aprovação e novas delações colocam em xeque a habilidade do governo peemedebista de atravessar o próximo ano. Estamos estudando as entrelinhas da constituição para determinar o que acontece depois que cai o rei de espadas, o de ouros, o de paus e não fica nada. Só de pensar que uma das opções é o FHC ser eleito indiretamente, provavelmente para governar como Imperador-Rei durante 100 dias, faz essa situação toda parecer um episódio do Mundo da Lua.

Já discutimos bastante nesse blog sobre a justiça das eleições (ver meu post sobre eleições indiretas e sobre formas de eleição), mas nunca dei minha opinião de qual era o meu método favorito, como eu gostaria que o presidente fosse escolhido em minha ilha particular. Vamos analisar os principais problemas de nossos métodos de eleição e pensar em uma maneira de driblá-los.

Nosso sistema atual de eleições diretas é realizado em dois turnos, o primeiro dito de escolha e o segundo de eliminação. Tentamos com ele evitar o maior problema de uma eleição a um único turno, que é a multiplicação de candidatos permitindo alguém com 20% dos votos levar a presidência. Mas esse método traz consigo outro problema, que é perfeitamente ilustrado na eleição francesa de 2002, aquela do famoso segundo turno Chirac vs Le Pen.

A França tem dois grandes partidos: LR (centro direita) e PS (centro esquerda). Há também uma constelação de partidos menores, entre eles o FN (extrema direita), cujo porta bandeira era Jean-Marie Le Pen em 2002 ((Desde então foi substituído por Marine Le Pen, MLP, sua filha, aquela que habita meus pesadelos, a não se confundida com My Little Pony ou Multilayer Perceptron)). O primeiro turno das eleições francesas de 2002 trouxe uma surpresa, o voto da esquerda foi dividido em diversos pequenos partidos e o candidato do PS, L. Jospin, ficou em terceiro, fechando o segundo turno como um combate entre Jacques Chirac (RPR na época, o partido depois virou UMP e depois LR) e J-M. Le Pen (FN). Para piorar, diversas pesquisas de opinião apontavam vitória de Jospin sobre Chirac em um possível segundo turno, se ao menos ele chegasse lá.

Em um movimento inédito, a esquerda apoiou Chirac em massa, e em desespero, o equivalente brasileiro ao PSOL, PT, PCdoB e PCO apoiarem Alckmin massivamente para impedir a eleição de Bolsonaro. O resultado do segundo turno era previsível.

chirac_lepenImagine o equivalente disso na competição de 100m rasos. Na Rio 2016, os favoritos ao título eram Bolt e Gatlin. Nada mais justo do que deixar todo mundo correr e ver quem chega na frente. Agora imagine que corredores menores podem aparecer, gente que não tem chance nenhuma ao título dados os resultados anteriores que apresentaram em torneios, e esses corredores ganham o direito de poder puxar Gatlin ou Bolt pelo shorts. Não parece um sistema ideal de avaliar um campeão olímpico, mas é bem próximo do que temos para avaliar presidente.

Qual a solução? Não queremos uma situação parecida, em que Jospin, um candidato com grandes chances de vitória, seja eliminado porque “seu voto” foi dividido entre opções menores da esquerda. Coloco aspas com cuidado, porque o voto não é dele, é do eleitor, mas essa é a percepção que esse raciocínio carrega. Não queremos forçar pessoas a votarem em quem “tem chance”, mas queremos um método em que a inclusão de candidatos menores não influencie no vencedor, essa é nossa primeira exigência.

Imaginemos então a seguinte situação: os candidatos Luís, Geraldo e Jair disputam uma eleição em dois turnos. No primeiro turno, temos Geraldo na frente com 45%, Luís com 30% e Jair com 25%. No segundo turno, contudo, pesquisas apontam que Luís vence Geraldo em um confronto direto. A solução para Geraldo é simples: ele faz um pouco de campanha por Jair, perde alguns votos, e garante que o segundo turno será entre ele e Jair, onde suas chances de vitória são bem melhores. Esse sistema também é absurdo, porque um candidato não deve melhorar sua posição perdendo votos, ou piorar sua posição ganhando votos! Essa é nossa segunda exigência.

O teorema da impossibilidade de Arrow, mencionado em outro post, diz, grosso modo, que nenhum sistema classificatório de candidatos é capaz de satisfazer esses dois critérios. A matemática não está a nosso lado, e a missão parece perdida.

Como todo bom matemático, se você quer violar um teorema, basta quebrar a hipótese certa na engrenagem correta. Eu usei de propósito a palavra classificatório para descrever os sistemas de eleição, porque isso é uma hipótese importante para a tal impossibilidade. Basta não exigir um sistema classificatório e podemos encontrar uma maneira de eleição que não sofra das mazelas que nossas duas exigências tentam sanar!

Ao invés de perguntar aos eleitores quem é o favorito, o que é uma simples classificação com apenas uma vaga, e ainda ao invés de perguntar a ordem de preferência, que é uma classificação mais complexa, passamos uma lista de todos os candidatos ao eleitor. Ao lado de cada nome, duas opções: ? ou ? . Após os votos, o candidato com mais ? ganha, simples assim.

De que maneira isso escapa das garras de Arrow? Cada candidato, em um sentido, compete contra si mesmo nesse método. Se A possui mais ?  que B, pouco importa se C, D ou E entram na corrida, a ordem de preferência ainda é mantida. E nenhum candidato em sã consciência tentaria aumentar suas chances de voto diminuindo seu número de ? , porque isso não funciona. Com um modelo quase facebookiano de eleição, temos, em minha opinião, bastante progresso em relação ao atual, e a complexidade não é muito maior.

Mas ainda não gosto muito desse modelo, podemos fazer melhor. Esse método estimula candidatos a instruírem eleitores a não apenas votar ? em si, mas votar também ? em todos os outros. Isso porque agrupa na mesma categoria candidatos que de alguma forma toleraria ver na presidência e aquela que eu realmente quero; também agrupa aqueles de que marginalmente desgosto e aqueles que abomino. Essa dicotomia não é saudável, e podemos evitá-la. O modelo fica um pouco mais complicado, mas tenho fé de que não o suficiente.

Como vou atribuir porcentagem e juízo de valores, vamos usar candidatos mais fictícios que Geraldo, Luís e Jair. Sejam Jon, Edward, Cersei e Tyrion quatro candidatos às eleições de Westeros. Cada eleitor receberá uma ficha com os quatro candidatos e, ao lado de cada nome, deve escolher uma nota de 1 a 5; ou uma avaliação dentre as possíveis: muito bom, bom, médio, ruim e muito ruim. Contados os votos, podemos empilhar as porcentagens da seguinte forma:

westeros_eleicao_1

Note que Cersei é a candidata mais polarizadora, ela possui a maior taxa de “muito bom” e a maior rejeição. Em uma eleição a dois turnos, imaginando que o “muito bom” representa o voto do favorito de um eleitor (não necessariamente verdade, alguém pode votar marcando todos como ruim e muito ruim, por exemplo), teríamos Cersei e Jon no segundo turno, com Jon vencendo o segundo turno se eu imaginar que ninguém votaria em um candidato que considera ruim ou muito ruim. Isso não é necessariamente o ideal, porque Jon e Cersei de longe são os candidatos de maior rejeição, mas é um das características mais famosas de nosso sistema atual de eleição.

O método conhecido como voto por aprovação consiste em passar uma linha nos 50% daquele gráfico. O vencedor da eleição será o candidato que possui a melhor avaliação na linha dos 50%. Em caso de empate, analisamos a “barra de avaliação” de cada candidato e o vencedor é aquele cujo ponto médio da barra é o mais alto. Esse sistema é mais simples do que parece, veja o que acontece quando traçamos essas linhas e esses pontos no gráfico.

westeros_eleicao_2

Claramente, Cersei está eliminada. Na barra dos 50% ela atinge a avaliação ruim, pior que nossos três outros candidatos. E como há empate entre esses candidatos na avaliação “médio”, marcamos o ponto médio da barra cor creme e percebemos que o mais alto é o de Tyrion, que é o vencedor segundo esse método.

  • Vantagens e críticas

O método não é perfeito, mas possui muitas vantagens. Em primeiro lugar, ele evita esse pensamento de “votar um muito bom e o resto muito ruim” porque, por exemplo no caso de Tyrion, alguém que votasse muito bom ou bom não faria diferença, ou alguém que ao invés de muito ruim votasse ruim também não influenciaria. Vale mais você usar dessa avaliação para expressar seu voto em toda sua complexidade. Eu, particularmente, votaria Edward muito bom, Tyrion bom, Jon médio e Cersei muito ruim, o que exprime com muito mais clareza minha opinião e me permite contribuir de forma mais completa ao processo democrático.

Esse sistema força eleitores a tomarem uma posição sobre todos os candidatos, o que é tanto uma vantagem quanto uma crítica. O número de candidatos não poderia ser muito alto, e jogado no mundo real esse modelo pode sofrer de maneira amplificada os problemas do analfabetismo político de boa parte da população. Qual avaliação dar a um candidato que não conheço? É uma pergunta complicada.

Por outro lado, ele dá muito mais chance a bons candidatos de partidos menores, porque todos os candidatos devem ser votados. Propaganda negativa nesse contexto não tem muito sentido, pois não existe mais voto para evitar que alguém seja eleito. Cada candidato deve convencer os eleitores de que ele é digno de seu voto, e não simplesmente convencer o povo de que o adversário é um vilão de filme da Disney.

“Mas, em seu exemplo, Edward deveria ter ganhado!”

Essa é uma crítica válida, porque Edward é menos rejeitado que Tyrion, especialmente na área do “muito ruim”. Mas o método atribui a vitória a Tyrion porque ele atribui o mesmo peso à rejeição que a aprovação. Note que 40% dos eleitores acham que Tyrion seria pelo menos bom (bom e muito bom), enquanto apenas 25% dos eleitores pensam isso de Edward. 30% do eleitorado acha que Tyrion é ruim ou pior, enquanto apenas 25% do eleitorado pensa isso de Edward. Como Tyrion ganha na aprovação por um valor maior do que Edward ganha na ausência de reprovação, a vitória vai a ele, essa é a ideia do centro da barra.

Um item suplementar, que seria um sonho nesse método, é colocar uma cláusula extra que diz que se todos os candidatos na linha dos 50% são classificados como ruim ou muito ruim, novas eleições deveriam ser chamadas e esses candidatos não poderiam se reapresentar. Visto que eles, em absoluto, são vistos como inadequados para representar o país, não podem governar.

 Esse método é muito bonito, e profundamente utópico. Não imagino que algum dia o Brasil adotará algo parecido, nem se qualquer outro país o fará em qualquer futuro. Ainda, vale a pena apreciar e imaginar o que seriam o processo eleitoral e a política se esse fosse o método, como seriam a propaganda, a estratégia, a tentativa de convencer o povo de que aquele candidato é, em absoluto, muito bom. Quando termino esse devaneio, essa contemplação do Brasil que não existe, volto à realidade e percebo que a discussão não está no método, mas em se haverá ou não eleição, voto, democracia e Brasil em 2017 e 2018. Comparando com o voto por aprovação, votar em um candidato parece pouco; no contexto atual da política, encontrar em quem votar parece muito.

1 resposta

E nossos filhos nos chamarão de bárbaros

Rookie

election

É difícil explicar a cadeia de sentimentos que me atingiu com a eleição de Donald Trump para a presidência dos Estados Unidos. Em primeiro lugar, feriu meu brio estatístico, eu estava disposto a apostar dinheiro alto em Hillary pelas projeções e pesquisas feitas exaustivamente por matemáticos e cientistas americanos, eles adoram essas coisas; e foi outro Brexit. Em segundo lugar, pelo desespero trazido pela realização que, Europa ou EUA, a esperança não é mais capaz de vencer o medo.

Sou, e sempre fui, um otimista. Sempre acho que meu ano presente é o melhor de minha vida, que a sociedade caminha em uma direção mais aberta, pluralista, receptiva e tolerante, que diversos direitos conquistados por minorias são agora inalienáveis e que a questão do racismo, da misoginia e da intolerância será naturalmente resolvida pela passagem inexorável das horas, pela morte, de velhice e pacífica, dessa geração criada com outros modos e outros costumes. Depois de hoje, não sei se sou capaz de levantar essa bandeira com tanta convicção.

É difícil generalizar esses eleitores, mas vou tentar assim mesmo. Sinto como se eles quisessem surrar com violência o establishment, Washington no caso dos americanos, e Trump era o punho. Sinto também, na Inglaterra e nos EUA, como se esse voto fosse o último grito de uma maioria branca que percebe no horizonte o fim de sua hegemonia e grita, esperneia, porque “cultura do país” e “sua cultura” não serão sinônimos óbvios. “Cultura branca” não é algo que existe, chamamos isso nesses países, infelizmente, de apenas cultura.

Porque ainda que tanto o Brexit quanto a eleição de Trump estejam fortemente correlacionados a raça, escolaridade e idade dos eleitores (brancos, sem ensino superior e acima de 50 anos votaram em bloco para o sucesso de ambos os cataclismos),  sei que o silêncio de um dos lados é tão culpado quanto o barulho do outro.

Eu me considero um liberal, em um sentido bem vago da palavra. Posto bastante sobre política, então evito falar de minhas opiniões para não perder credibilidade, mas Donald Trump não é exatamente uma questão de opinião. Essa vitória chocante é um evento nauseante na história da democracia americana, um homem carregado ao poder por forças de nativismo, nacionalismo, misoginia e racismo. Trocam o primeiro presidente negro por um charlatão que sugou apoio de áreas xenofóbicas e de supremacia racial branca. É impossível reagir a esse evento com algo menor que repulsa. E ainda, apesar de todos os escândalos, apesar de todos os absurdos, os eleitores odiaram mais o que ele dizia combater do que seus hábitos horripilantes, e pagaram para ver o que estava “atrás da porta número 3”, como se em um programa de auditório, ao invés de uma mulher competente com história de vida pública, talvez história até demais.

Li uma vez um artigo no Le Monde cujo título me marcou bastante, ele dizia: “Et nos enfants nous appelleront: ‘barbares'”, ou, na minha tradução fraca, o título desse post. Ele me faz pensar em qual é o papel de alguém que se diz progressista, alguém que deseja estar do lado certo da história. Não é apenas, como alguns pensam, defendem direitos estabelecidos e claros, mas buscar novos. Nossa tarefa, nessas derrotas tenebrosas, nesses tempos sombrios, é erguer a cabeça e continuar lutando contra os males de hoje e de amanhã. Meu objetivo é não me tornar como minha avó, uma pessoa maravilhosa e mulher progressista em seu tempo, mas que não era capaz de admitir que Rui Barbosa era pardo, tampouco Machado de Assis.

Pensamos na escravidão, na ditadura militar, na repressão da era Vargas, na segregação americana e no Apartheid africano, no papel das mulheres durante toda a antiguidade até mais ou menos 1970, em homossexuais sendo castrados quimicamente, condenados à morte, em transexuais atravessando uma vida de repressão e culpa, e pensamos: “Bárbaros!”. Nossa tarefa não é apenas combater os males de hoje, não é apenas ter um amigo negro, ou um chefe gay, e achar que racismo e homofobia não se aplicam a você. Nossa tarefa é pensar: “por que meus filhos me chamarão de bárbaro?”, como eu chamo minha avó, e ela chamava, provavelmente, sua avó. Respondendo essa pergunta, você descobre o mal a combater.

Eu queria poder postar algo científico, estatístico, sobre a vitória de Trump, analisando detalhes da sondagem e apontando os pontos fracos, mas o fato é: ninguém sabe o que aconteceu. Explicações sobram, mas quando já se sabe a resposta fica bem mais fácil. Talvez as pessoas que mais votariam no Trump também seriam as que mais desconfiariam da mídia golpista que ligaria para fazer uma sondagem, o que criou uma sub-representação de trumpistas em três ou quatro estados chave, o suficiente para o sistema americano colapsar. Prometo um post sobre a forma de governo americana, e sobre como ela é particularmente ruim, para aparecer semana que vem.

É bom estar de volta, queria que as circunstâncias fossem outras.

5 respostas

Ondas gravitacionais

Rookie

Estou atrasado para comentar algo sobre ondas gravitacionais, mas esse atraso tem dois motivos. O primeiro é a saturação da mídia, é difícil achar algo para escrever que já não tenha sido escrito, e melhor, sobre o tema; e o segundo é eu já ter comentado isso no alarme falso de ondas gravitacionais que tivemos em 2014.

Dessa outra vez, como todo o resto da mídia, empolguei-me antecipadamente, caindo no grande erro de cantar vitória antes do peer-review. Esse episódio serve de lição no que é o centro da ciência: a ideia da autocorreção, e de não ter medo de dizer que está errado. Comento isso em outro post, nesse vamos ver o experimento LIGO, o que fez e o que mediu.

O artigo você encontra aqui. Vou tentar contar a história que o artigo apresenta sem a linguagem técnica, que nem eu entendo tão bem, não sou astrofísico, mas meu curso de relatividade geral no mestrado vai me servir de algo. Em setembro de 2015, o observatório LIGO (Laser Interferometer Gravitational-Wave Observatory), encarregado de medir alterações no campo gravitacional em sua volta, detectou um forte sinal. Ele possui dois detectores, um em Washington e um em Louisiana, e é importante ter dois detectores para diferenciar o que é ruído e o que é sinal. Todo detector, como antena de televisão antiga, possui ruído, e ondas gravitacionais são tão difíceis de medir que apenas eventos que produzam alguma alteração considerável na gravidade podem vencer o ruído e ser medidos. O sinal medido foi esse:

LIGO_data_1O eixo x, cortado do gráfico, representa intervalos de 0.05s nos ticks maiores. Na esquerda você vê o sinal medido em Washington e na direita, Washington e Louisiana sobrepostos. Pelo gráfico da direita você consegue ver que o começo do sinal ainda está cheio de ruído, há áreas em que eles não concordam nem um pouco, mas a partir do meio do gráfico há forte coincidência nos sinais, uma oscilação acelerando, crescente, e uma queda brusca na intensidade. Esses 0.1s de sinal são o que físicos esperavam faz 100 anos, desde que Einstein formulou a relatividade geral e propôs que a gravidade, como o eletromagnetismo, deve produzir ondas.

Essas ondas não são algo fácil de explicar ou entender sem alguma matemática, mas vou tentar. Gravidade, como descrita pela relatividade geral, é uma deformação do espaço-tempo. Eu sei que sem nenhuma equação isso parece mais uma frase de terapia de autoajuda quântica que ciência séria, então tente imaginar que gravidade acontece porque a massa dos corpos afeta o espaço em torno do corpo e atrai outros corpos para si. Quanto maior a massa, maior é esse efeito. Se um corpo massivo acelera, ele afeta o espaço em torno de si de um jeito um pouco diferente, ele perturba esse espaço com sua gravidade e essa perturbação pode se propagar.

Em uma analogia, uma grande explosão de dinamite libera energia que atinge as moléculas no ar, elas se propagam atingindo outras moléculas no ar, que atingem outras, e outras, até atingirem o frágil osso em nosso tímpano e registramos isso como um barulho alto. A gravidade se comporta de um jeito parecido, mas, diferentemente do som, ela é extremamente fraca, o que pode ser entendido na analogia como se fôssemos praticamente surdos. Apesar de nossa audição comprometida, Einstein previu faz cem anos que o som existe, e estamos tentando medi-lo ou detectá-lo de vários jeitos, tentando criar um aparelho auditivo cada vez melhor. Um dia, uma explosão acontece, e temos um excelente aparelho auditivo (o LIGO); finalmente, e pela primeira vez, conseguimos ouvir algum som do universo. Esse som você vê na figura acima.

E isso é diferente de simplesmente “detectar gravidade”, porque isso detectamos o tempo todo. Se você pular do quinto andar, certamente detectará mais gravidade do que gostaria, essa medida é de uma natureza diferente. Ainda na nossa analogia com som, é como se soprassem forte em seu rosto. Você consegue sentir vento e sopro sem problemas, detectar ar e movimento de ar não é a questão. Mas som é outra coisa. Som é a propagação de vibrações no ar causadas por objetos à distância, e ele carrega informação sobre esses objetos, é bem diferente de vento e brisa. Eu sinto por qualquer astrofísico que esteja lendo essa analogia entre gravidade e vento, mas foi o melhor que pude fazer.

Vale a pena discutir um pouco como esse tal de LIGO funciona. Ele tem dois braços (cada um de 4 km cada), um perpendicular ao outro, e cada braço possui um laser que vai e volta esses 4 km. Quando uma onda gravitacional passa, ela deforma o braço, porque altera a gravidade sutilmente e essa alteração faz a interferência entre os lasers mudar ligeiramente, mas o suficiente para medir uma alteração muito pequena. A sensibilidade de LIGO é excepcional, ele é capaz de detectar uma diferença no tamanho dos braços de uma distância menor que um núcleo atômico.

Depois de medir esse sinal, os cientistas usaram uma boa análise comparativa para diminuir o ruído e dar aquela alisada nos dados, todos nós físicos somos versados na arte de alisamento, chapinha e escova de dados experimentais. O resultado é:

LIGO_2Agora sim isso está bonito. Tendo o sinal bonito e alisado, que são as linhas cinza desses gráficos, resta fazer o trabalho de detetive. Pela primeira vez escutamos um som com nossos ouvidos, mas que barulho é esse? O que produziu esse som? Parece ambicioso querer saber a natureza do barulho logo na primeira vez que escutamos qualquer coisa, mas poucas coisas no universo são capazes de produzir um ruído desse calibre, então podemos listar as mais prováveis e ver qual melhor se encaixa no que escutamos.

Ondas gravitacionais são produzidas por objetos massivos acelerados, isso sabemos. No espaço, a única fonte de aceleração possível para um corpo massivo desses (tirando a expansão do universo e tal) é a presença de outro corpo massivo que, pela sua gravidade, puxa aquele primeiro. E o primeiro puxa também o segundo. Assim como o Sol puxa a Terra, a Terra também puxa o Sol, mas é mais ou menos um cabo de guerra entre uma criança de cinco anos e um levantador olímpico de peso, o Sol nem se mexe. Quando dois corpos bem massivos se encontram, de massas comparáveis, nenhum ganha no cabo de guerra e, ao invés de um orbitar o outro, ambos orbitam um ponto comum em uma bela dança conhecida como sistema binário, algo assim:

E isso causa alterações na gravidade em forma de ondas periódicas, exatamente o que o LIGO mediu, então é uma boa sugestão que esse sinal tenha vindo de um sistema binário. Mas a frequência e a intensidade do sinal aumentam e colapsam, terminando em uma linha praticamente reta como o sinal cardíaco de alguém em seu último suspiro. O que poderia ter causado esse fim ao sistema binário? A solução mais simples, os corpos do sistema binário se encontraram e viraram um só.

Um sistema binário costuma ser bem estável, assim como a Terra girando em torno do Sol é um sistema, felizmente, bem estável. Mas ao longo das centenas de milhões de anos esse sistema vai perdendo energia, muito em parte por emitir as tais ondas gravitacionais, e essa perda de energia faz os corpos irem se aproximando nessa dança. Chega uma hora que os parceiros desse baile se encontram, e a explosão monumental que ocorre foi o que o LIGO mediu. Pelos dados que temos, e pela teoria que sabemos, podemos medir a massa e o tamanho desses corpos massivos que, no final da dança, se fizeram ouvir pelos quatro cantos do universo: são, sem dúvida, dois buracos negros em um sistema binário que colidiram e se tornaram um.

Não há analogia possível para esse evento. Posso apresentar números, mas nada que qualquer cérebro humano seja capaz de conceber, de tentar entender. Um evento nessa proporção foge do que nosso cérebro foi condicionado para imaginar. Posso dizer quantas centenas de bilhões de bombas nucleares isso representa, mas essa analogia tanto é sem sentido quanto ainda está longe de representar a grandeza em termos de energia dessa colisão. Temos sorte de não estar nas redondezas, de não ver de mais perto o evento, essa explosão monumental, essa mostra de poder do universo, esse Krakatoa do cosmos.

Com os grandes progressos da análise computacional e de modelos calculáveis de relatividade geral, podemos simular em nossos computadores os valores desse explosão, programar em C++ o nosso próprio Krakatoa, e ver que tipo de onda gravitacional sairia disso. É com bastante alegria que digo que isto são as linhas coloridas do gráfico anterior, alinhando perfeitamente com o que foi medido. A história desse evento, que aconteceu todo em menos de um segundo, com buracos negros de massa dezenas de vezes maiores que o Sol se movendo a metade da velocidade da luz, é dada por esse gráfico:

LIGO_3E foi isso que foi medido entre Washington e Louisiana em setembro de 2015.

Eu gosto muito de física, e é difícil segurar o fascínio, e um pouco da emoção (sou clichê assim mesmo), quando contemplo algo parecido. A medição traz algo de pessoal a esse fato. Eu certamente conseguiria conceber uma colisão de estrelas, de buracos negros ou de galáxias teoricamente, eu já fiz exercícios na faculdade de coisas parecidas, mas isso tudo é impessoal, teórico demais; é muito diferente de de fato medir algo assim, saber que aconteceu, onde e quando.

Poderia parar o post por aqui, mas tenho recebido várias perguntas de “para que isso serve?”. Tenho minha resposta favorita a essa pergunta, mas resisto porque sei que nem todo mundo tem esse gosto pela coisa. Mantenho a analogia com a audição: ganhamos um sentido novo. Podemos medir coisas que antes não eram possíveis. Há diversos objetos que não interagem de forma eletromagnética, em especial matéria escura e energia escura (são “escuras” com um motivo), mas que interagem de forma gravitacional. Podemos agora ter esperança de medir eventos e objetos que apenas quem tem ouvidos pode escutar. Claro, ainda estamos na infância disso, nosso aparelho de audição pode melhorar bastante, ele ouviu algo porque a explosão foi bem grande, mas é um começo. O universo está rico em sons gravitacionais de várias fontes, e de várias formas, e, pela primeira vez, estamos escutando.

3 respostas