Moda é algo difícil de explicar. Em ciência e tecnologia, todo ano temos assuntos que são mais comentados, esperados, publicados, as modinhas científicas do momento. Em 2000 tínhamos a palavra cyber, em 2005 era a web 2.0, em 2010 só se falava em big data. De todas essas modas, nunca vi nada parecido com a atual. Ela transcende a moda, vejo-a em artigos de física, matemática, informática, na mídia, em palestras, até na apresentação do próximo telefone que vou comprar. Como ela faz parte de meu trabalho, chegou o momento de explicar o que é deep learning. Vou tentar fazer isso com a menor quantidade de matemática que consigo, deixo para outro post a explicação com matemática pura, sem gelo e sem limão. Primeiro, explico o que é essa história de learning. Depois, explico o que o deep quer dizer.
Essa história de learning
Aprender é ver alguém fazendo alguns exemplos e conseguir não apenas reproduzir o que viu, mas aplicar o que viu em casos que ainda não viu. Essa capacidade de lidar com casos não vistos durante o treinamento é a marca do aprendizado genuíno, chamamos isso de generalização. Em poucas palavras: entendimento é previsão que pode ser generalizada. Um aluno que só é capaz de resolver na prova as questões que ele viu na lista de exercícios não aprendeu nada. Ele memoriza, mas não entende.
Uma prova pode ser entendida, matematicamente, como uma função que leva perguntas em respostas. Todo aprendizado estatístico, seja deep learning, machine learning ou reinforcement learning, consiste apenas nisso: associar uma resposta a uma pergunta, achar a melhor função que leva nossas questões às boas soluções tanto nas situações em que nosso modelo foi treinado (a lista de exercícios), mas para outras situações em que ele não foi treinado (a prova final).
Então toda essa história de machine learning e deep learning é a arte de achar a melhor função para explicar um conjunto de dados. Em espírito, não são muito diferentes de, dados alguns pontos, encontrar a melhor reta que passa por eles. Toda a literatura científica desse meio, se você quiser ofender quem trabalha na área, pode ser resumida em técnicas mais ou menos sofisticadas que traçar retas complicadas por uma quantidade bem grande de pontos.
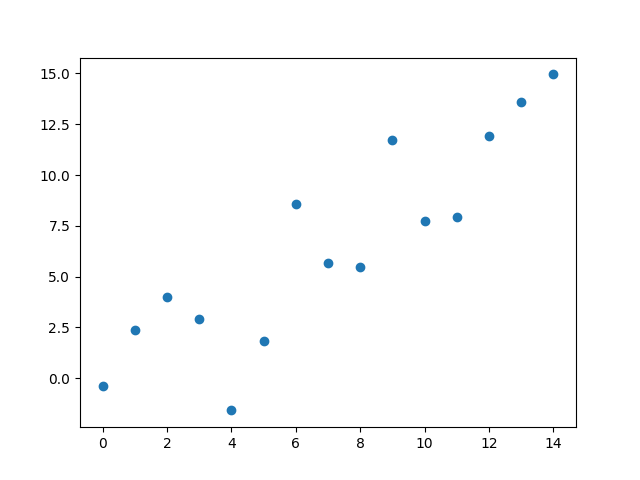
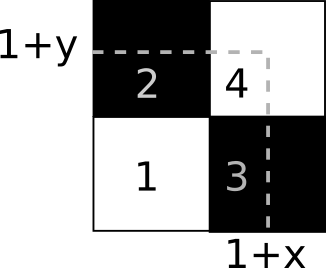
Vamos direto para o exemplo, então. Precisamos de pontos para traçar uma função, e eu proponho esses:
O problema é bem simples: precisamos da melhor função que poderia servir como o “modelo teórico” que gerou esses dados. Nossa mentalidade é a de que existe um mecanismo subjacente simples o suficiente para ser expresso com uma função, a que buscamos, e a diferença entre os pontos de nossa experiência e nossa função vem apenas de pequenas flutuações naturais que não conseguimos, ou não pretendemos, explicar ou incluir no modelo. Como se esses pontos fossem nossas medidas de quanto tempo um peso leva para chegar ao chão em função da altura que deixamos ele cair. Existe uma lei por trás disso, a da gravidade, mas há pequenas flutuações possíveis no resultado quando faço a experiência: minha velocidade de reação no cronômetro, resistência do ar ou o erro mecânico do relógio.
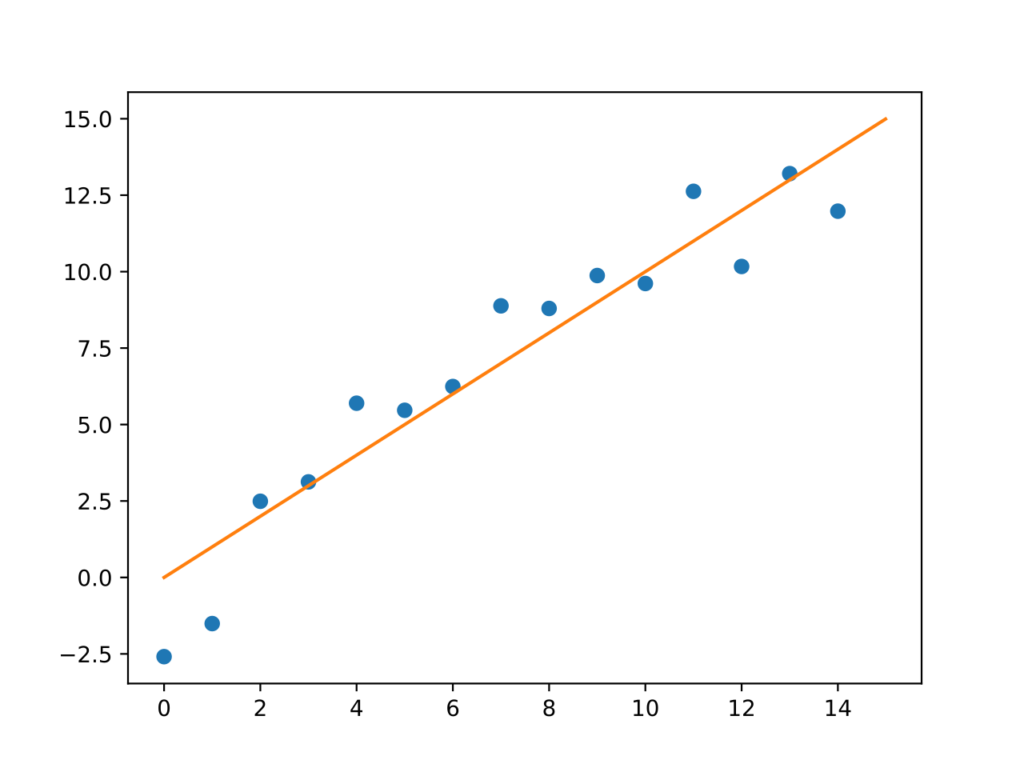
Sem um modelo, fica bem difícil resolver esse problema. Tenho muitas opções para explicar esses pontos, eis algumas:
- Linear
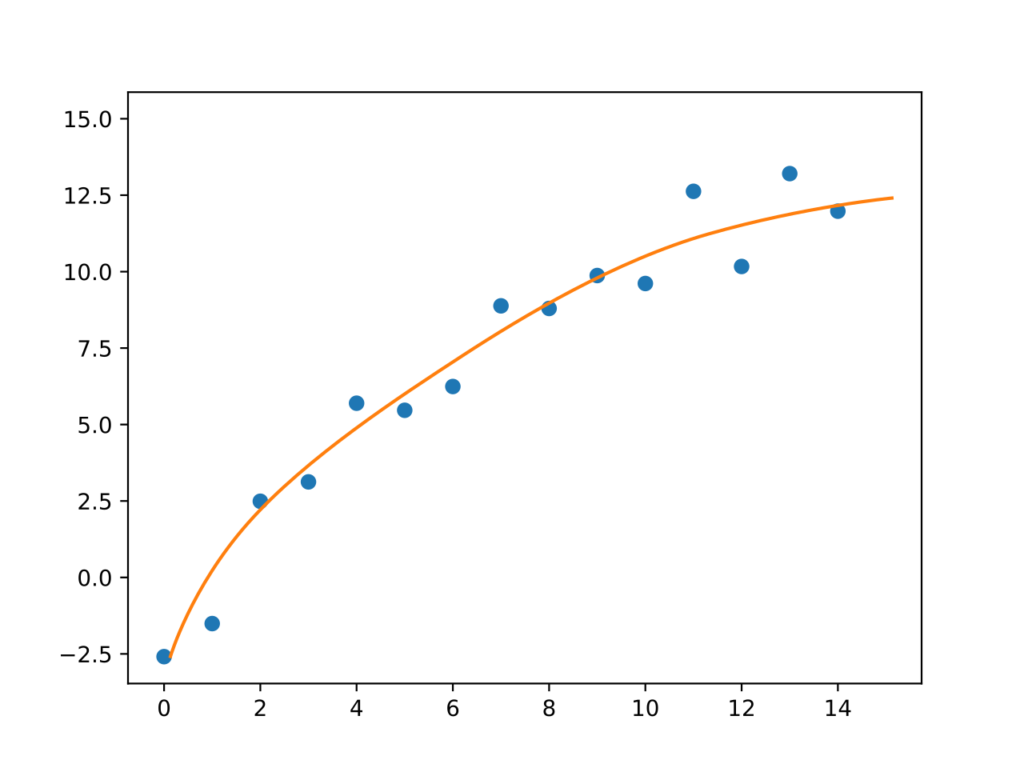
- Parábola
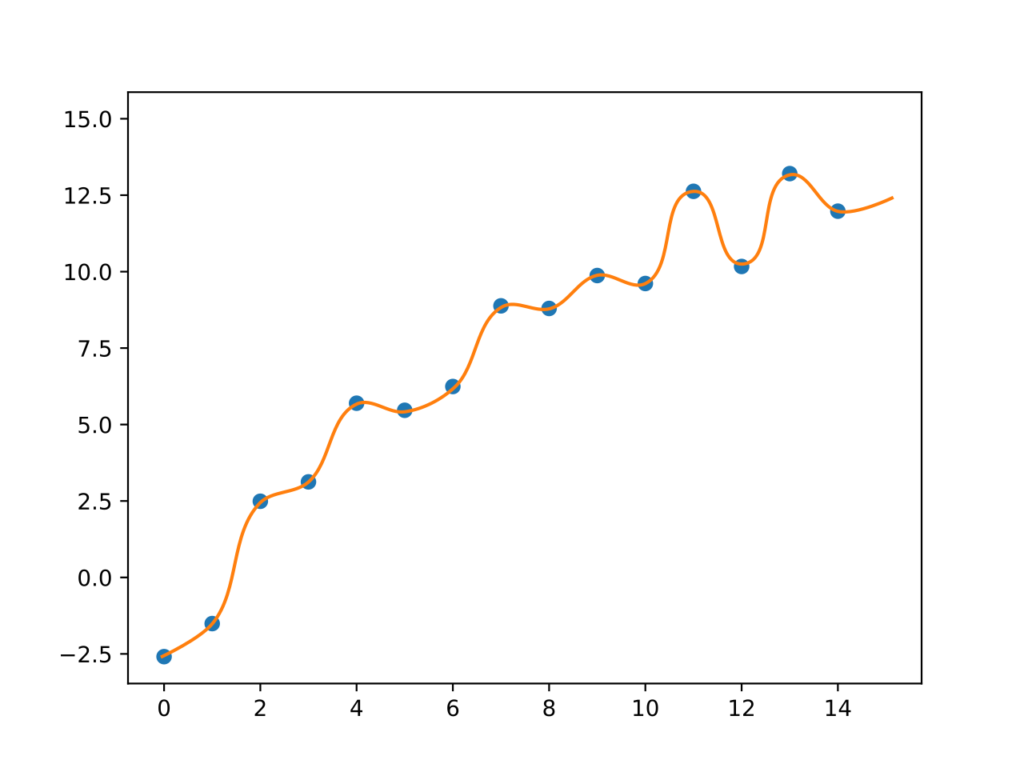
- Polinômio completo
Todo caminho é bom para quem não sabe para onde ir. Não vou entrar em detalhes de como escolher uma dessas opções se você não conhece muita coisa sobre o modelo, vou apenas pegar o caso mais simples e supor que o modelo certo é uma reta. Para descobrir qual a melhor das retas possíveis, preciso especificar dois parâmetros: inclinação e altura. Existem maneiras de encontrar exatamente, com apenas uma equação, quais parâmetros criam a reta que mais bem explica os dados ((Para quem fez exatas, o método dos mínimos quadrados está aí para isso)), mas não pretendo usar uma dessas soluções exatas. Elas só funcionam quando o problema é fácil, como traçar uma reta, qualquer método ligeiramente mais sofisticado precisa de ajuda que nenhuma resolução exata consegue fornecer. Vamos usar uma abordagem iterativa, mais parecida com o que o deep learning usa, e muito mais próxima do conceito de aprendizado.
Nossa reta terá dois parâmetros: $\alpha$ e $\beta$. Nosso modelo será descrito pela equação $y = \alpha x + \beta$, preciso apenas encontrar os parâmetros que fazem dessa curva a melhor possível. Pense nesses parâmetros como um botão daqueles de aparelhos de som profissionais, que você pode aumentar e diminuir gradualmente. Eu começo com os valores dos parâmetros aleatórios. O resumo da estratégia é: pego um ponto, vejo se acertei. Se errei, o que é provável, vejo para que lado tenho que girar o botão de cada parâmetro para melhorar o resultado. Giro e repito o processo para o próximo ponto.
A ideia é bem simples: tento, erro, vejo para onde devia andar para errar menos, ando, repito o processo. O quanto eu mexo do botão a cada iteração, o tamanho do passo que dou, varia e depende de meu problema. Nesse contexto, chamamos de taxa de aprendizado, ou learning rate, porque tudo é importado do inglês nesse meio; e o nome da técnica é descida de gradiente (chamamos de gradiente a direção que temos que mexer os parâmetros para diminuirmos o erro do modelo). Vamos aplicar essa técnica em nosso problema:
A ideia é mais simples do que parece. Começamos com um ponto aleatório, e por acaso pegamos o segundo ponto. Traçamos uma reta qualquer. Depois, pegamos outro ponto ao acaso, que foi o sétimo, e corrigimos a reta para também passar nele. Em seguida, pegamos outro ponto e fazemos a reta andar mais na direção dele. Essa direção é guiada pelo sentido do erro calculado usando a reta como modelo. Se o erro é positivo, enviamos a reta mais para baixo. Se é negativo, mandamos a reta mais para cima. Depois de usar vários pontos, a reta muda pouco e temos um modelo que tenta, na medida do possível, satisfazer todo mundo.
Esse processo de apresentar exemplos ao modelo e ir corrigindo pouco a pouco é o que chamamos de aprendizado estatístico, é a base da palavra learning nessa história de deep learning. A reta não é a única maneira de traçar um modelo, há várias, o deep learning fornece uma delas que é particularmente poderosa para alguns problemas específicos. Se ao invés de pontos simples nós tivéssemos que encontrar um modelo que leva um conjunto de pixels, uma imagem, a um valor, que representa o conteúdo da imagem, uma reta teria bastante dificuldade em fazê-lo. Nisso entra nosso convidado de hoje, a aprendizagem profunda.
Essa história de deep learning
Nosso problema agora é esse: tenho 15 pixels, organizados em uma rede 5 x 3. Eles apenas possuem valores 0 e 1, preto e branco. Com eles, posso desenhar formas bem primitivas. Estou bem interessado em números, como aqueles do seu relógio digital velho. Por exemplo:
Meu objetivo é: dados esses pixels, qual número parece estar escrito neles? Não parece uma tarefa difícil, até você pensar no que essas imagens significam para o computador. Cada uma delas é uma de 32768 configurações possíveis de tabelas com quinze coordenadas cada, sendo cada coordenada um zero ou um. Para o computador, essas imagens são:
Se eu não ligar para invariâncias espaciais ((Eu deveria ligar! É possível, e recomendado, usar técnicas de aprendizagem profunda que levam em conta invariâncias translacional e rotacional. Estou ignorando aqui para simplificar as coisas.)), essas imagens são vistas pelo computador como:
[1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0]
[1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0]
[0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0]
[1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0]
[1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0]
[1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0]
[1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0]
[1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0]
[1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0]
[1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0]
Aqui fica claro que é bem complicado interpretar esses números como imagens, e é isso que queremos fazer nosso modelo aprender. Quero uma função que leve cada conjunto de quinze coordenadas binárias em um valor entre zero e nove de forma razoavelmente precisa. Não há reta que resolva. A reta fica perdida sem entender as complicadas correlações entre pontos distantes ou próximos. Esse é um ponto que pretendo desenvolver em outro post, mas menciono aqui: métodos clássicos estatísticos focam em descobrir correlações de caráter mais simples entre os dados. A grande vantagem do deep learning é a possibilidade de descobrir correlações e padrões bem mais complicados.
E o que, afinal, é isso? Deep learning envolve o uso de um modelo chamado rede neural. Para nosso modelo anterior, o dos pontos, chutamos uma relação linear com dois parâmetros $y = \alpha x + \beta$ e pareceu funcionar bem. Primeiro, vamos imaginar como seria um jeito de tentar resolver o problema dos dígitos usando uma reta. Temos quinze valores de entrada, então uma “reta” com quinze variáveis (ela na verdade vira um plano) seria:
\[ y = \alpha_1 x_1 +\alpha_2 x_2 +\ldots +\alpha_{15} x_{15} +\beta \]
Por mais que eu mexa nos $\alpha$’s e no $\beta$, não há jeito ou maneira de fazer $y$ acertar os valores, mesmo se eu arredondar seu valor para virar um número inteiro. Os padrões do meu problema não são lineares, não existe uma correspondência clara de “quando um pixel aumenta, o valor do dígito aumenta”. Se queremos capturar uma relação mais complicada entre entrada e saída, precisamos de mais poder de fogo. Uma rede neural é exatamente isso: uma função mais complicada que a reta e com mais parâmetros para acertar, ainda que a ideia geral seja a mesma.
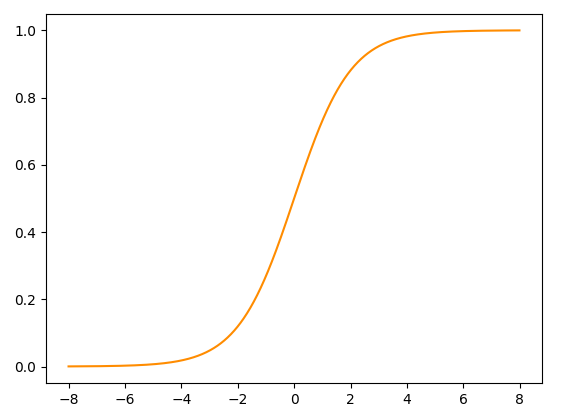
A rede neural consiste em pegar os quinze elementos de entrada e aplicar uma sequência de operações lineares e não-lineares. Uma operação linear é uma que envolve só soma e multiplicação, como aquela que eu usei acima para definir a “reta”. A ideia é pegar os elementos de entrada, fazer aquela operação do $\alpha_1 x_1+\ldots +\alpha_{15}x_{15}+ \beta = z_1$ e depois fazer o resultado dessa operação, que eu chamei de $z_1$ passar por alguma função não-linear que dê uma torcida nos resultados. A função não-linear escolhida para compor o valor dos $z$’s varia. Vamos pegar uma escolha clássica, a função sigmoide, que tem essa cara:
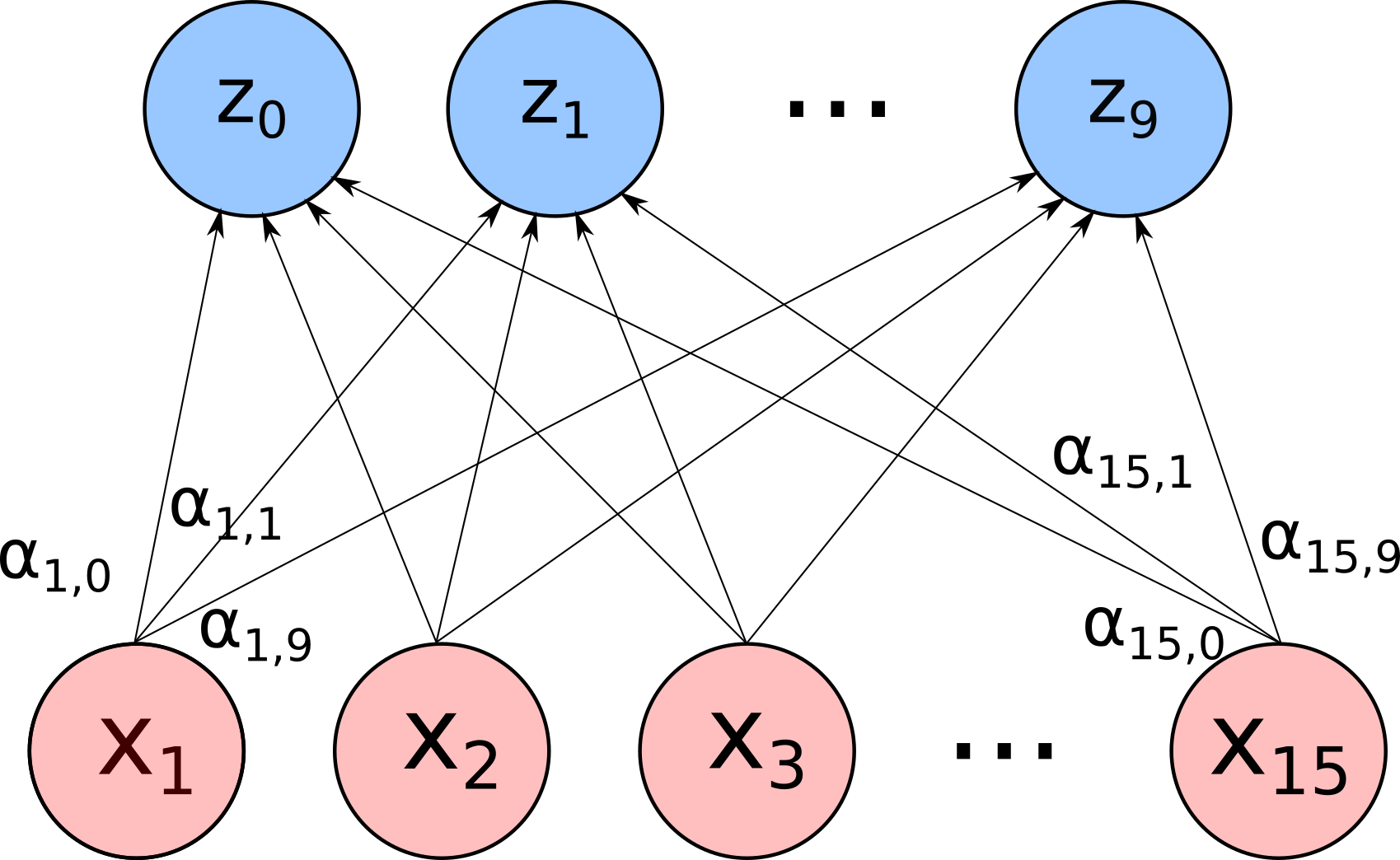
Não vou fazer isso uma vez apenas, vou fazer isso dez vezes diferentes. Ou seja, vou criar uma coleção de dez $z$’s, cada um calculado a partir das mesmas entradas, mas com coeficientes $\alpha$ diferentes. Uma imagem vale mais que esse parágrafo, a ideia é fazer uma conta assim:
Onde cada linha representa um $\alpha_{i,j}$ que multiplica a entrada $x_i$ e leva para a composição do $z_j$. Depois eu vejo qual dos meus $z$’s tem o maior valor. Se é o $z_3$, por exemplo, então digo que esses pixels correspondem ao número 3. É como se essas operações tentassem, através de combinações complicadas, definir qual $z$ é o vencedor dados esses pixels. Escolhendo o vencedor, tenho a previsão do modelo.
Parece complicado, mas realmente não é. Estou apenas multiplicando as entradas por números (os $\alpha$’s), somando, passando por uma função um pouco mais torta (a sigmoide), e colecionando o valor que dá como resposta. Terei assim 150 valores diferentes de $\alpha$’s e 15 $\beta$’s para acertar, tunar, mexer como um ladrão experimenta com a maçaneta do cofre para encontrar a combinação certa. Não vou acertar esses coeficientes na mão, claro, não sou capaz disso. Uso o mesmo método de antes: pego um ponto, vejo se acertei, vejo em qual direção eu teria que mexer os coeficientes para minha previsão chegar mais perto da resposta certa, mexo, repito o processo.
Minha função final agora é pegar o maior valor de dez possibilidades, sendo cada uma delas uma combinação das entradas com 16 parâmetros diferentes (15 $\alpha$’s e 1 $\beta$). Ela é bem mais complicada, mas me permite capturar relações mais complicadas. Com o modelo linear, a “reta”, eu tinha apenas 16 parâmetros para acertar, agora tenho 165. Isso me dá bastante espaço para aprender as sutilezas dos pixels, mas ainda não é o suficiente. Preciso de mais poder de cálculo, mais parâmetros. Preciso ir mais fundo nessa rede neural para tentar aprender alguma coisa.
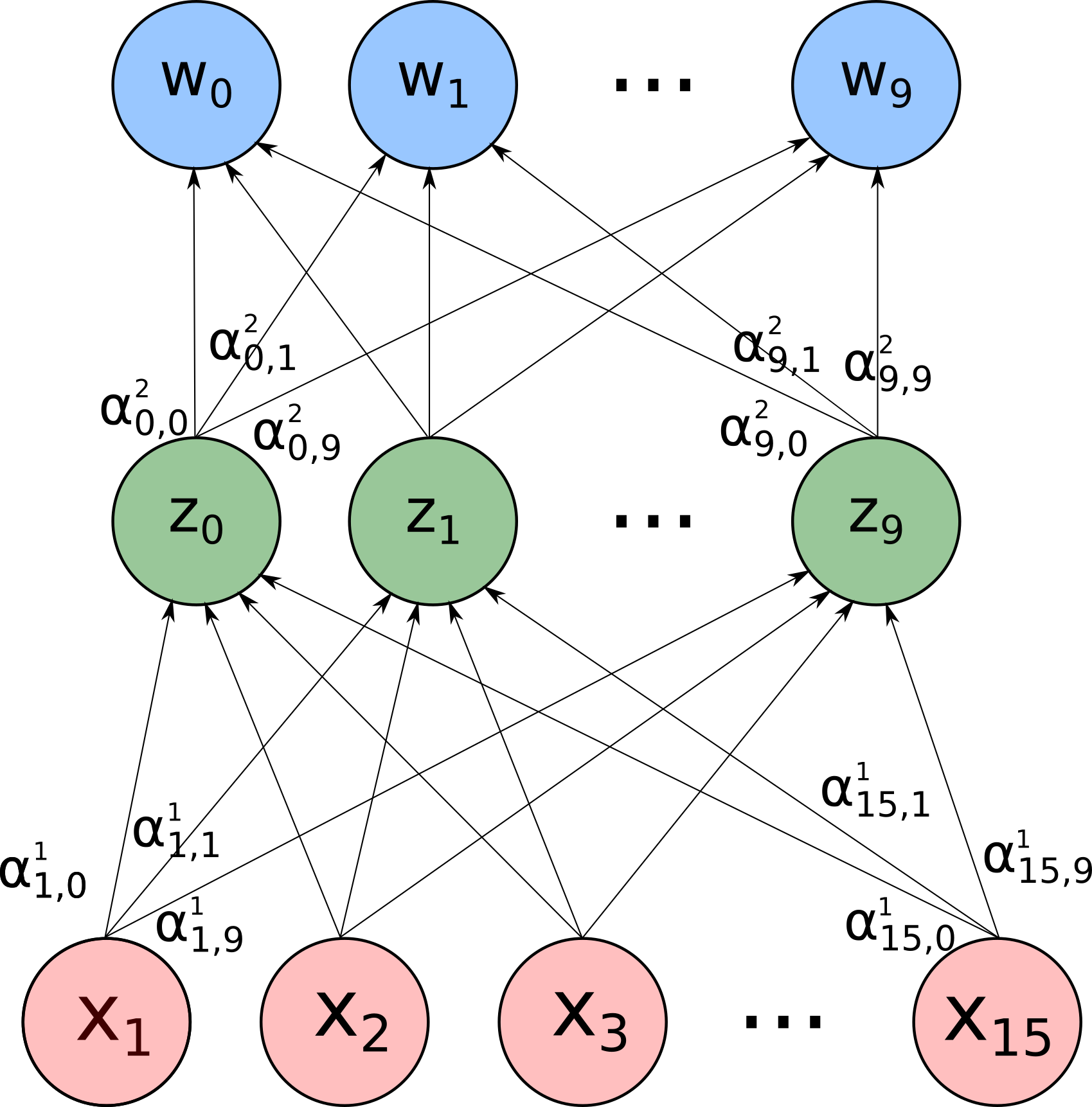
Essa transformação dos valores de entrada em operações lineares e não-lineares para formar os $z$’s é chamada de camada. Para criar um modelo de aprendizagem profunda, a ideia é usar os $z$’s como entradas de uma próxima camada. Essa concatenação de camadas é o que dá o nome de deep learning. A imagem talvez deixe as coisas mais claras:
E por fim, você vê qual dos $w$ é o maior e elege ele como a previsão do modelo. Se o dígito deveria representar um 4 e o maior valor é o $w_4$, você acertou. Se errou, calcula para onde os parâmetros, que agora são 275, devem ser mexidos para você obter um $w_4$ mais elevado.
Isso funciona?
Por incrível que pareça, sim, mas ninguém sabe direito porquê. Os elementos de resposta que temos são bem complicados e deixo para um post geek ou hardcore, o de hoje termina com você brincando com a rede neural que eu descrevi acima. Gerando um monte daqueles dígitos, treinamos os 275 parâmetros e temos uma coleção de $\alpha$’s e $\beta$’s que talvez sejam capazes de entender quando uma imagem é um dígito. Tente você mesmo, na planilha abaixo, produzida por meu grande amigo Gabriel Rovina:
REDE NEURAL TREINADA PARA VOCÊ SE DIVERTIR
Salve uma cópia local (Arquivo -> Salvar uma cópia) dessa planilha para poder editá-la. Em seguida, brinque com o número na entrada, acendendo e apagando os pixels para formar o dígito que deseja. Não é um sistema perfeito, você pode não concordar com alguns resultados dele, mas é bem certinho na sua capacidade de deduzir o que é cada dígito.
Isso é deep learning, nada mais, nada menos. No final, temos uma função complicada que é uma combinação de somas, produtos e passagem por sigmoides, com muitos parâmetros para acertar usando aquela estratégia de tentar, errar, corrigir e tentar de novo. É um sistema bem eficaz para análise de dados cujos padrões são complicados de extrair, especialmente imagens, sons e linguagem. Planejo um post futuro, mais geek ou hardcore, para aprofundar nos motivos de funcionamento de deep learning e em quais problemas ele não funciona de jeito nenhum. Por enquanto, divirta-se com essa rede que eu preparei na planilha, e não me xingue se você formar algum número que ela não reconhece. Com menos de 300 parâmetros e sem invariância espacial, foi difícil fazer coisa melhor.