Entreguei o manuscrito de tese na madrugada entre sexta e sábado. Foi um grande alívio, e o fim de uma etapa muito feliz de minha formação. Se tudo correr bem, em outubro serei dotô em física e parto, em novembro, para o departamento de sistemas complexos do Instituto Weizmann, em Israel. Isso significa, acima de tudo, que retomo o blog! E no post de hoje, tento comentar um pouco sobre o que foi minha tese.
É complicado falar do meu trabalho aqui, porque criei esse espaço exatamente para falar de coisas distantes de minha pesquisa quando minha pesquisa não estava muito interessante. Correlações entre políticos, aniversários de jogadores de futebol, Banco Imobiliário, cassino de Parrondo, tudo isso é muito legal, mas não enche barriga e não coloca artigo na mesa. Minha tese parece mais chata, mais estranha, mais fora da realidade, mas é ciência sendo feita e precisa de um pouco de contato com o meio para entender seu propósito, sua razão de ser.
Minha tese, no final das contas, fala de um tipo de partícula, férmions. Provavelmente todas as partículas que você lista na sua cabeça, prótons, nêutrons, elétrons, são férmions. Elas têm uma propriedade fundamental, chamada Princípio de Pauli, que diz que dois férmions não podem ser “idênticos”. Se colocados exatamente no mesmo lugar, eles têm que diferir em alguma coisa. Na ausência de opções, os férmions assumem níveis de energia diferentes. Ou seja, é impossível colocar um bocado de férmions juntos em energia bem baixa, você sempre acaba vendo eles se agrupando com mais energia do que deveriam, apenas para preservar esse princípio de Pauli.
Se você jogar um monte de férmions em um vale, eles naturalmente vão rolar para o fundo do vale. Mas eles não podem ficar todos no fundo do vale, então alguns são obrigados a ficar alguns níveis acima do ponto mais baixo do vale. É como se eles se repelissem, como se não quisessem ficar juntos, respeitando o princípio de Pauli. Minha tese é exatamente sobre esse fenômeno de repulsão, e sobre como essa repulsão afeta as flutuações da quantidade de férmions em uma região do vale.
Pode parecer algo meio artificial, mas não é fácil explicar a motivação do negócio em algumas linhas assim. Esse estudo é importante para entender aspectos de sistemas quânticos como intrincamento em escalas maiores que microscópicas, e até dá para checar experimentalmente.
Você define um pequeno intervalo, uma caixinha, e conta quantos férmions caem naquele intervalo. Esse número flutua, e você pode estudar o quanto ele flutua. É bem legal estudar como essa flutuação aumenta ou diminui quando o tamanho do intervalo aumenta. Digamos que esse intervalo seja $I=[-L,L]$. Quando $L$ é bem pequeno, já era sabido que essas flutuações aumentavam com o logaritmo do tamanho do intervalo, então $\mathrm{Var}(N_L)\propto \log L$, sendo $N_L$ o número de férmions na caixa e $\mathrm{Var}(N_L)$ suas flutuações. Quando o intervalo é muito grande, todos os férmions caem dentro dele e não há mais variação, então para $L$ grande $\mathrm{Var}(N_L)\to 0$. De $\log L$ a zero alguma coisa estranha aconteceu, e minha tese responde, pela primeira vez, o que exatamente aconteceu. Embaixo desse paŕagrafo, coloco o gráfico completo dessa transição!
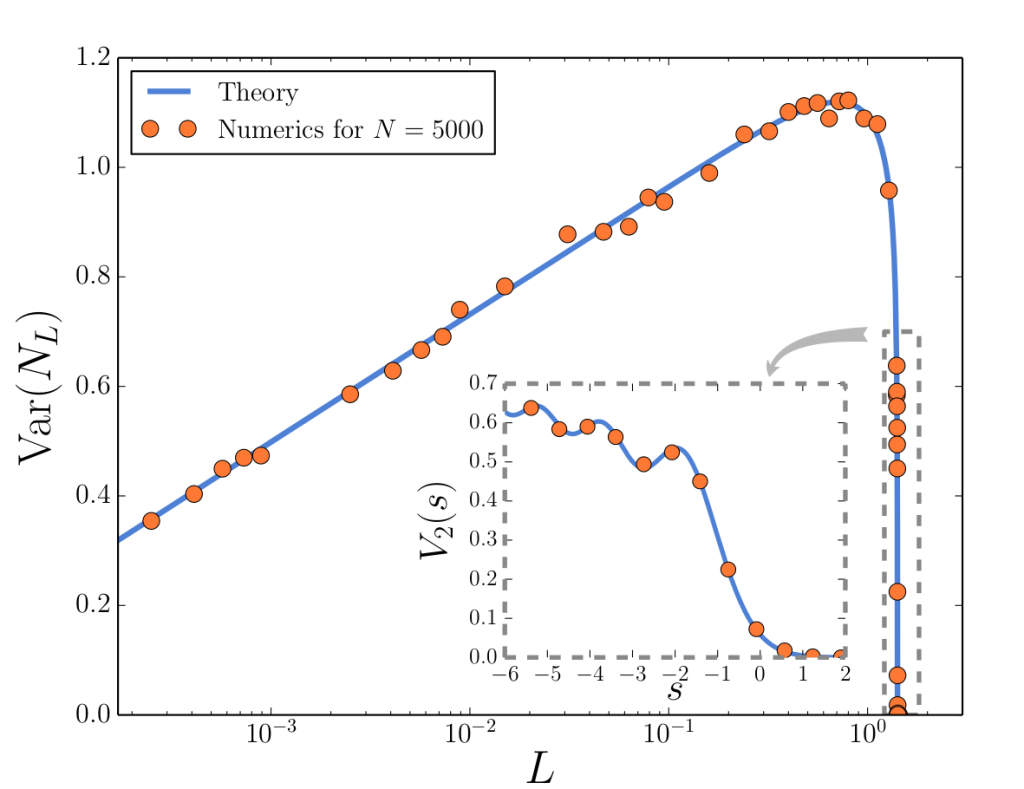 Bonito, não? Esse gráfico é uma das “descobertas” da minha tese, e fico bem feliz com ele. Temos a função teórica azul, que é bem bonita, temos esse comportamento oscilatório dessa parte cinza que damos um zoom e temos a função de como essa linha azul continua depois disso. Tudo deu bastante trabalho, mas o resultado final me deixou bem feliz.
Bonito, não? Esse gráfico é uma das “descobertas” da minha tese, e fico bem feliz com ele. Temos a função teórica azul, que é bem bonita, temos esse comportamento oscilatório dessa parte cinza que damos um zoom e temos a função de como essa linha azul continua depois disso. Tudo deu bastante trabalho, mas o resultado final me deixou bem feliz.
Não espero que você tenha entendido tudo, nem metade, esse post é mais uma catarse, um desabafo do fim de um período muito divertido, interessante e querido da minha vida. Minha tese de doutorado termina e o pós-doutorado começa. A partir de agora, eu vou virar um pesquisador de verdade, as pessoas até vão achar que sou um especialista no assunto. Quero ver até quando, um mês, um ano, cinco anos?, as pessoas vão acreditar em toda essa mentira de que eu sei o que estou fazendo.
