Arquivo mensais:janeiro 2013

Reality show

Rookie

Todo mês de janeiro, vejo não apenas minhas mídias sociais, mas também portais sérios de notícias e meios de comunicação serem invadidos por notícias de um reality show. O Big Brother costuma ocupar por três meses aquele espaço que os jornalistas não conseguiram preencher, dissertando cada detalhe do que pessoas extremamente convencionais fizeram ontem e hoje, levando pessoas em um sofá a se fascinarem vendo outras pessoas sentadas em um sofá.

São um fenômeno moderno, pois seria muito difícil antes de 1950 se obter tais equipamentos de vigilância sobre pessoas. E, confesso, não fazem jus ao nome, não é possível se dizer um retrato da realidade se as pessoas, sabendo das câmeras e microfones, agem de acordo, quebrando a magia da espontaneidade. Por isso, cada vez que leio sobre BBB, ou sobre qualquer outro desses, penso no primeiro, mais honesto e mais interessante de todos os reality shows: Farm Hall. Também conhecido pelo codenome “Operação Epsilon”, Farm Hall faz Boninho parecer uma criança amadora. Para entender esse reality, precisamos entender um pouco de física nuclear.

Ao final da segunda guerra mundial, os aliados e o eixo disputavam uma corrida científica acirrada em busca da arma suprema que definiria o combate: a bomba nuclear. Qualquer lado que a obtivesse primeiro, tendo condições de lançar, poderia mudar o curso da guerra, e da história mundial. O lado dos aliados é bem conhecido, em Los Álamos eles juntaram os maiores gênios da física nuclear e de partículas jamais reunidos, encabeçados pelo gênio italiano Enrico Fermi e aquele que se chamaria de destruidor de mundos, J. R. Oppenheimer. Eles conseguiriam pouco a pouco controlar as reações nucleares e canalizarem essa tecnologia na forma da arma suprema, infelizmente lançada no fatídico agosto de 1945 contra o Japão.

O eixo, contudo, tinha seus campeões: Otto Hahn, Max von Laue, Weizsacker,  entre outros, somando dez ao todo, liderados pelo gigante da física Werner Heisenberg. O projeto alemão da bomba atômica avançou, eles sabiam que a bomba era possível; ainda, antes que pudessem conceber a arma, os dez maiores físicos da Alemanha foram capturados pelos aliados na capitulação alemã.

Os aliados não sabiam, no entanto, o quanto esses homens sabiam da bomba atômica, e o quão perto os alemães estavam de produzir aquela arma. Para descobrir, entre julho de 45 e janeiro de 46, eles colocaram esses dez cientistas em isolamento completo em uma casa no interior da Inglaterra, com microfones escondidos espalhados em toda a casa. Começaria o primeiro Reality Show da história, e provavelmente o mais interessante.

A casa de Farm Hall.

As transcrições de Farm Hall são fascinantes. Após um mês de confinamento, os cientistas recebem notícias, através de um jornal, do bombardeamento de Hiroshima e Nagasaki. Otto Hahn, um dos descobridores da fissão do urânio, contempla suicídio; Max von Laue, um grande opositor do regime nazista, comemora não terem conseguido terminar o projeto. Mas a grande pergunta, e a que torturava Heisenberg, era a mais simples: onde eles haviam falhado? Como os americanos haviam conseguido?

Frente à notícia do lançamento da bomba, Heisenberg reage furioso, alegando ser falsa. Uma semana depois, organiza uma espécie de conferência improvisada, usa o jornal como referência e começa um colóquio para definir onde estava o erro alemão. Essa discussão não é apenas interessante do ponto de vista histórico, ela é uma aula de física nuclear, literalmente, eu tive minha aula de fissão nuclear usando trechos das transcrições de Farm Hall. Ao invés de explicar como funciona a fissão, deixo Heisenberg o fazer, citando a abertura de sua conferência a seus colegas prisioneiros:

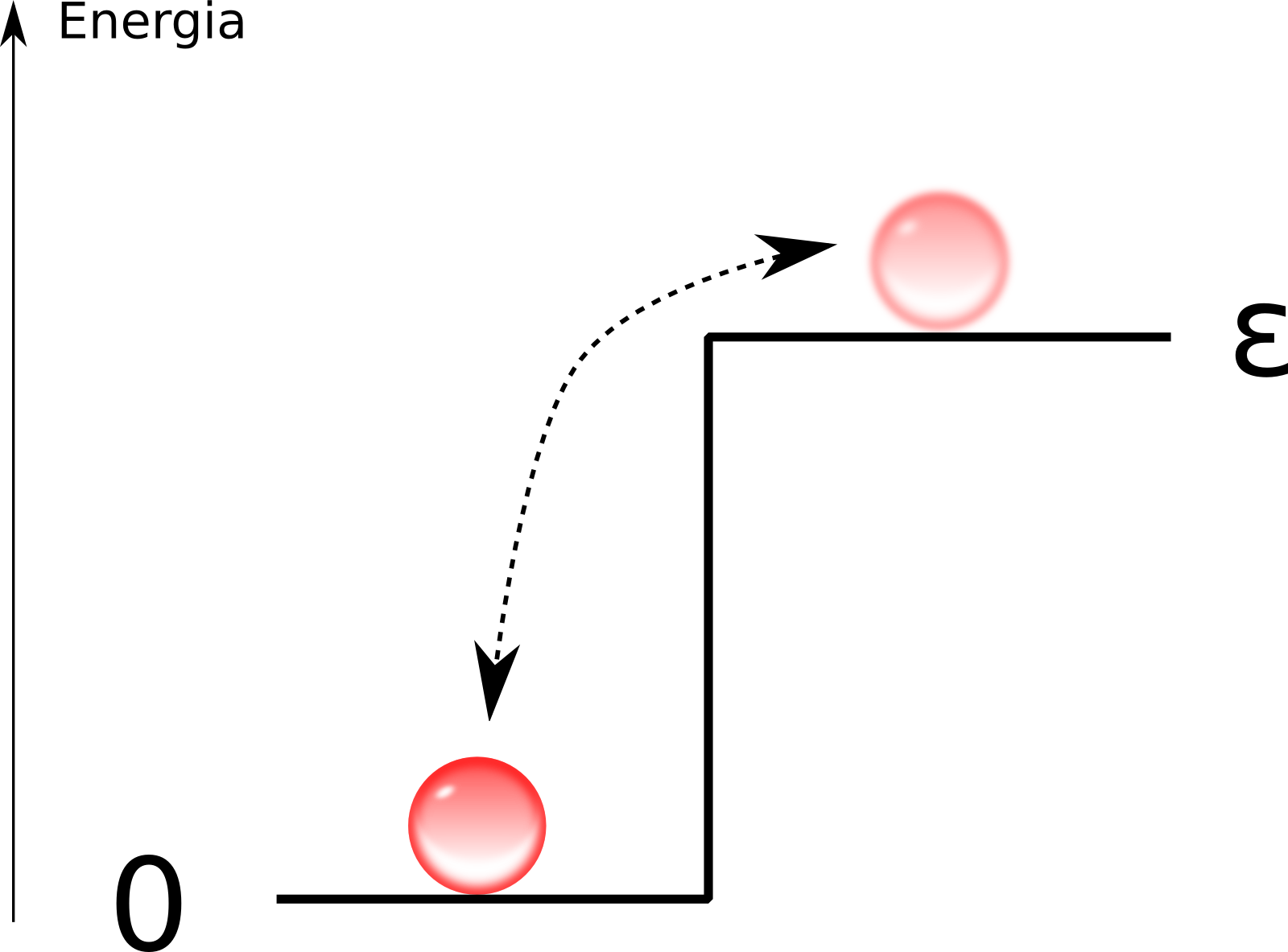
HEISENBERG: Vou começar recapitulando, mais uma vez, os principais dados envolvendo o U235 (urânio com massa 235, altamente radioativo). Vou dizer rapidamente o que acontece, talvez, nessa bomba. Um nêutron presente no U235 encontra, bem rápido, em seu percurso, um outro núcleo de U235. Duas coisas podem acontecer: ou ele é difundido elasticamente (ricocheteado, sem perder energia), essa difusão pode ser elástica ou inelástica, ou ele causará a fissão (quebra) do núcleo. Se é difundido, ele parte com uma velocidade muito similar à que chegou, e isso não altera o fato de que ele provavelmente provocará a fissão de um outro núcleo em seguida. A probabilidade de perder nêutrons é então nula. O processo ocorre naturalmente até o nêutron encontrar um núcleo de U235 e quebrá-lo. Nessa fissão, outros nêutrons são produzidos, e uma reação em cadeia se inicia. Se tivéssemos uma quantidade infinita de U235, ela jamais pararia, pois cada fissão produz de 2 a 3 nêutrons. Esses nêutrons continuariam o processo, e o número de nêutrons aumentaria exponencialmente. No entanto, a produção de nêutrons está em competição com o processo de fuga de nêutrons da massa. De fato, como a massa que possuímos é finita, os nêutrons que são produzidos na superfície e cuja velocidade inicial aponta para fora irão escapar e não participarão da fissão. A questão que se coloca é se essa perda de nêutrons consegue superar a produção, e qual é a massa mínima para que a reação ocorra e cause uma explosão.

A figura a seguir fica por minha conta:

Heisenberg acaba descobrindo seu erro, e, noto, seu orgulho deve ter ficado abalado, pois não foi nada muito sofisticado. Cometendo um erro que aflige todos os físicos, usou sua intuição no sentido errado e, simplificando um termo para facilitar suas contas, desprezou um valor importante demais e acabou calculando que a massa de urânio necessária para a bomba seria milhares de vezes maior do que o real valor. Isso diminuiu muito o interesse alemão em tentar desenvolver a bomba, pois tal quantidade de urânio enriquecido seria impraticável, muito cara e levaria muito tempo para ser produzida.

O erro de Heisenberg foi achar que valores médios podem substituir valores reais. Ele conseguiu medir o percurso médio de um nêutron no urânio, e sabia a velocidade média do nêutron. Com isso, ele tinha um tempo médio que o nêutron levava para atingir um urânio, e com isso conseguia calcular quantos nêutrons seriam produzidos por segundo. Eis o erro, essa multiplicação é uma simplificação grosseira demais, dizimada pelo fator exponencial da produção de nêutrons. Usar os valores médios despreza o fato de que os primeiros nêutrons produzidos afetarão outros átomos de urânio, que afetarão outro, em uma reação em cadeia que privilegia claramente os nêutrons produzidos no início. Um processo exponencial não pode ser analisado com valores médios, você precisa tomar um grande cuidado, escrever a equação diferencial da difusão e incluir um termo de geração de nêutrons adequado. Heisenberg calculou esse valor usando apenas movimento Browniano e valores médios, superestimando o valor da massa crítica da bomba e matando boa parte do incentivo governamental para a produção da arma.

Outros fatores impediram o projeto alemão. Heisenberg tivesse talvez percebido seu erro se possuísse medidas precisas de grandezas nucleares, mas isso foi em grande parte impossibilitado pela guerra da água. Para medir grandezas nucleares em fissão, você precisa de alguém para absorver os nêutrons quando quiser parar a reação e não arruinar sua experiência. Os alemães usavam um material conhecido como água pesada, que é água convencional com mais nêutrons do que devia. Esse material era produzido como resultado da fabricação de fertilizante, mas ele exige uma quantidade colossal de energia e o único país com essa disponibilidade energética era a Noruega, com suas grandes hidroelétricas. Em operações especiais de espionagem e sabotagem dignas de filme, os aliados conseguiram desativar a usina hidroelétrica norueguesa na Operação Gunnerside, e forças de resistência norueguesas afundaram o barco que transportaria a água pesada restante à Alemanha.

A história da física nuclear é fascinante, com momentos de aventura e tragédia, contendo Farm Hall como um dos mais interessantes exemplos do perigo que representa um cientista que sabe demais. Nunca se confirmou o real interesse de Heisenberg na construção da bomba, mas suspeito que nem era esse o motivo de tanta fúria ao saber que outros tinham construído. Acredito que ele queria menos que os alemães tivessem a bomba do que saber a razão de seu erro, saber onde os americanos haviam acertado, saber qual de seus cálculos estaria errado.

Farm Hall também possui trechos emocionantes, como quando a casa recebe a visita de Sir Charles Darwin, físico, neto do biólogo, e Otto Hahn pergunta se ele tem notícias de sua família. Por fim, coloco um último trecho, com uma parte do dilema moral dos cientistas alemães, tirado daqui e traduzido livremente:

HEISENBERG: O fato é que toda a estrutura do relacionamento entre os cientistas e o estado alemão era tal que não estávamos 100% interessados em fazer, e, do lado deles, o estado confiava tão pouco em nós que ainda que quiséssemos, não teria sido fácil conseguir.

DIEBNER: Porque os oficiais estavam interessados em resultados imediatos. Eles não queriam trabalhar com políticas a longo prazo, como os americanos.

WEIZSAECKER: Ainda que tivéssemos tudo o que quiséssemos, não era nada certo que teríamos chegado tão longe quanto os americanos e ingleses estão agora. Não há dúvidas de que estávamos tão próximos quanto eles, mas é fato que estávamos convencidos que a coisa não ficaria completa durante a guerra.

HEISENBERG: Bom, isso não é completamente verdade. Eu diria que estava completamente convencido da possibilidade de fazer um motor a urânio, mas nunca pensei em fazer uma bomba, e do fundo do coração eu estou aliviado que era um motor e não uma bomba. Preciso admitir isso.

…

WEIZSAECKER: Não acho que devamos criar desculpas agora por não termos conseguido, mas temos que admitir que não queríamos conseguir.

WIRTZ: Acho característico que os alemães fizeram a descoberta e não usaram, enquanto os americanos a usaram. E preciso dizer que não achei que eles ousariam usar.

Eis um reality show cujo pay per view eu compraria com gosto. No entanto, meu Facebook, os portais de notícia e os assuntos de meus amigos foram invadidos por outro, não por Heisenberg ou Weizsaecker, mas por Anamaras e Dhominis; não por dramas reais de pessoas geniais, mas por intrigas e personagens tão pífios que podemos até desejar, no auge de frustração e raiva, uma solução nuclear para tudo isso.

Deixe um comentário

Abaixo de zero

Rookie

Sempre fico feliz quando uma notícia da física atinge o grande público, quando a mídia decide que algum descoberta forma uma frase de efeito digna de manchete, e nessa semana não foi diferente. Um grupo de físicos do Instituto Max Planck conseguiu criar um gás a temperatura negativa, abaixo do zero absoluto, e isso provocou manchetes muitas vezes enganosas e, apesar de algumas matérias terem saído interessantes, a maior parte era apenas um agregado de traduções de versões americanas feitas por quem não entende do assunto.

Temperaturas negativas não são novidade na física, elas têm até página na Wikipédia, e pretendo hoje, nesse post, tentar explicar o que queremos dizer com isso, e tentar esclarecer confusões lançadas pelas matérias sensacionalistas de física de folhetim. Para isso, precisamos entender o que é temperatura.

No princípio hesitei se poderia explicar esse tópico sem antes falar de um conceito fundamental da termodinâmica, e de toda a física, a entropia. Temia descobrir, enquanto escrevia, que eu mesmo não entendia o assunto, pois é uma das noções mais escorregadias da ciência. De forma extremamente simplificada, entropia é a medida da desorganização de um sistema. Preciso de um exemplo tão simplificado quanto minha explicação, vou usar um sistema a dois níveis de energia. Dificilmente encontramos algo na vida real que seja isso, mas pouco importa, quero apenas explicar o conceito. Imagine um sistema com $N$ partículas, sendo cada partícula capaz de estar em um estado de energia zero ou em um estado de energia $\varepsilon$.

dois_estados_2Se todas as bolinhas estiverem confinadas no estado zero, esse sistema tem entropia zero. Se todas estiverem confinadas no estado $\varepsilon$, o sistema também terá entropia zero. Mas se elas puderem se mexer, variar de um estado a outro, essa entropia será um valor maior, e positivo, indicando que o sistema não mais possui aquela ordem perfeita de antes e agora é uma mistura estranha de estados. A entropia indica quão bem feita é essa mistura, sendo máxima quando todas as configurações do sistema, todas as combinações de bolinhas em cima e embaixo, são possíveis e igualmente prováveis, ou seja, desordem completa, não posso afirmar nada sobre o estado atual do sistema, ele pode ser qualquer coisa.

A temperatura é a medida de quanto a entropia de um sistema varia quando damos energia a ele: quanto menor a temperatura, mais desorganizado um sistema fica com energia. Naturalmente, quanto maior for a temperatura, menos desordem um sistema ganha com a energia.

O fato da temperatura ser sempre positiva em nosso cotidiano é um reflexo da propriedade natural do aumento de entropia com o aumento de energia, como arrumar sua casa perfeitamente e lançar dentro dela uma ratazana raivosa, o equivalente da energia; dificilmente a casa ficará ainda mais organizada. Assim, apesar de sistemas com alta temperatura ganharem pouca entropia com energia, eles não perdem entropia.

Se deixamos nosso sistema de bolinhas a dois níveis interagir com o meio externo, ele poderá trocar energia com o meio e as bolinhas ganham ainda mais liberdade de subir e descer a ladeira. Se o sistema e o meio externo são muito diferentes quando entram em contato, eles vão trocar energia até que o quanto um sistema é desordenado pelo ganho de energia seja igual ao quanto o outro também é, ou seja, até que as temperaturas sejam iguais.

Isso é reflexo do princípio de máxima entropia, uma noção física que vai além das bolinhas e partículas, ligada profundamente a teoria da informação e probabilidades. Mais uma vez de forma bem simplificada, ele diz que, se você não tem uma boa razão para proibir um estado, o sistema atingirá esse estado e, se não tem uma boa razão para diferenciar dois estados, o sistema atingirá os dois com a mesma probabilidade. Em nosso problema das bolinhas, o sistema trocará energia com o meio externo até que o quanto ele causaria de desordem cedendo energia seja igual ao quanto ele ganharia de desordem ganhando energia, porque dessa maneira a entropia do processo todo (sistema + meio externo) será a máxima possível. Dessa forma, quando as temperaturas são iguais, isso significa que tanto o conjunto sistema + meio externo pode ocupar o maior número de estados possíveis de energia.

Como um gás lançado em uma sala vazia tende a se dispersar, não a se concentrar, porque eu não tenho uma boa razão para impedi-lo de ir para qualquer lugar da sala. Ele tende a ocupar todo o espaço e a chance de encontrar uma partícula em qualquer lugar é a mesma: isso é o princípio da máxima entropia. Se você conectar essa sala a uma outra vazia, pouco a pouco o gás vai ocupando também a outra sala até que todos os estados possíveis sejam ocupados com a mesma probabilidade.

Pelo princípio da máxima entropia, o gás tende a invadir a segunda sala e ocupar todo o espaço. A probabilidade de que ele fique todo na primeira sala é infinitamente pequena.

Se deixamos o sistema acoplado ao meio externo em uma temperatura fixa, ele trocará energia com o meio externo, e a temperatura será o quanto de desordem ele vai ganhar quando ganha energia. Se essa temperatura é baixa, o sistema ganha muita entropia com um pouco de energia. Isso acontece em situações como a de haver todas as bolinhas paradas na posição 0. Dar um pouco de energia significa permitir alguns saltos para o andar de cima, isso bagunçaria o sistema dando bastante entropia a ele. Se o sistema está em alta temperatura, como no caso de um gás quente, dar ainda mais energia não bagunçaria tanto o sistema.

Podemos escrever isso com alguma matemática. A chance de uma daquelas bolinhas estar em um estado de energia $E$ é dada por $\frac{e^{-E/T}}{Z}$, onde $e$ é um número especial entre 2 e 3 e $Z$ é alguém que multiplicamos para que a probabilidade não seja maior que 1 (para quem começou a ver física estatística, essa é a distribuição de Boltzmann!). É fácil ver que a chance de estar no estado de energia 0 é $1/Z$, enquanto a chance de estar no estado $\varepsilon$ é $\frac{e^{-\varepsilon /T}}{Z}$. Isso representa um fato físico famoso: é mais fácil estar em um estado de baixa energia que em um de alta energia. Quanto menor a temperatura, mais difícil é encontrar alguém em um estado de energia alta. Quanto maior a temperatura, mais ambos os estados ficam com probabilidades parecidas. A maior parte dos sistemas físicos funciona dessa exata maneira.

No entanto, se você conseguir ser malandro, como os físicos do Instituto Max Planck, e criar um sistema físico bem patológico tal que estados de energia mais alta são mais prováveis, como você explica usando esse formalismo? Ora, basta dizer que são estados a temperatura negativa. Dessa forma, $\frac{e^{-\varepsilon /T}}{Z}>1/Z$ e você consegue continuar a trabalhar com esses sistemas usando sua matemática favorita.

É porque associamos temperatura a essa taxa de ganho de desordem que podemos interpretar desse jeito estranho. Temperatura não é mais o movimento das partículas, isso ficou com os gases ideais no colegial, ela agora é a medida do ganho da desordem em função da energia. E se um sistema começa a privilegiar estados de energia alta, interpretamos isso como uma temperatura negativa.

Ouvi muito a respeito, inclusive da Wikipédia, sobre a temperatura negativa ser o limite de uma temperatura tão positiva que ela “dá a volta” e vira negativa. Como dizer que os reais são um corpo cíclico me causa urticária, tento explicar o que isso significa. Uma temperatura muito baixa favorece muito estados de baixa energia. Uma temperatura alta não favorece ninguém, e quanto mais alta, menos favorecimento possui. Se atingíssemos a temperatura $+\infty$, teríamos passado de uma situação de favorecimento das energia baixas a não favorecer ninguém. Se fôssemos “além” do $+\infty$, teríamos uma situação que privilegia as altas energias, e é isso que aquela explicação estranha quer dizer. Não gosto dela, e paro a explicação da explicação por aqui.

Resumindo: os cientistas do Instituto Max Planck conseguiram criar um sistema patológico o suficiente para deixar os estados de alta energia mais prováveis que os de baixa energia. Na matemática da física estatística, isso é interpretado como uma temperatura negativa, pois temperatura é o que mede essa preferência por estados de baixa energia. Isso não é nada chocante ou escandaloso, é interessante que eles tenham conseguido isso para um sistema quântico bem complicado, o artigo original está aqui, mas, infelizmente, é mais uma manchete para vender jornal que um grande avanço para a termodinâmica.

Assumo que o post ficou confuso, mas é um tema complicado. Um dia sento e escrevo algo mais claro sobre entropia, no mesmo dia em que tomar coragem para ler a montanha de textos a respeito da interpretação física dela. Precisaria selecionar, ler, escrever, revisar tanta coisa que, em matéria de desordem, deixo exatamente como está.

4 respostas