Como todos, joguei bastante Banco Imobiliário em minha infância. Sonhava em morar em Morumbi ou Interlagos, tinha medo de algum dia passar perto da Av. Presidente Vargas, e com ele descobri o significado da palavra “revés”. Gostava, ainda que nunca tenha efetivamente terminado uma partida, sempre me solidarizava com os que empobreciam, deixávamos que continuassem, como se capitalismo e misericórdia combinassem, não dava certo.
Mas sempre fui assombrado pela busca pela tática ótima de se jogar esse jogo, se havia alguma. Inspirado em um estudo que li recentemente, dedico esse post a responder a grande pergunta: quais as casas em que mais paramos em uma partida? Assim, saberemos quais cores de propriedades precisamos, a todo custo, comprar ao parar.
Apesar de esse estudo já ter sido feito, não gostei da apresentação, nem da maneira como foi escrito; refaço-o, torcendo para que poucas pessoas achem, desse post, o que achei do estudo.
Para explicar como farei esse cálculo, preciso começar com um caso mais simples de jogo. Se Quico criou o xadrez para principiantes, apresento a vocês o Banco Imobiliário para iniciantes, ou, para criar uma temática, o Banco Imobiliário Zona Leste, referente à zona leste da cidade de São Paulo (figuras de Pedro Vergani, o mesmo que fez o banner do blog e diversas outras figuras desse blog):
Não há grandes surpresas nesse jogo. Usamos uma moeda e tiramos no cara-ou-coroa quantas casas andaremos: cara nos faz andar uma casa, coroa nos faz andar duas casas. Queremos analisar qual a casa mais provável de se cair e, para isso, precisamos trazer artilharia pesada da álgebra linear.
Vou precisar de uma matriz. Adoro matrizes, trabalho com elas e revolto-me com alunos de colegial que desdenham das aulas em que tiveram que aprender a “multiplicar tabelas”. Não os culpo tanto assim, é de fato bem estúpido querer multiplicar uma tabela por outra sem dar uma razão decente para isso, e hoje lhes apresento uma. Vamos criar a matriz estocástica do Banco Imobiliário Zona Leste. As regras para a matriz são: na primeira linha e segunda coluna, por exemplo, colocamos a probabilidade de, estando na primeira casa, cair na segunda casa. Como vocês sabem, essa probabilidade é ½ (tirar cara). A primeira linha dessa matriz será, portanto: 0, ½, ½, 0; ou seja, a chance é zero de ficar no mesmo lugar (você vai se mover), ½ de avançar uma casa (cara), ½ de avançar duas (coroa) e zero de avançar três. A matriz total será:
\[M=\left(\begin{matrix}0&\frac{1}{2}&\frac{1}{2}&0\\ 0&0&\frac{1}{2}&\frac{1}{2}\\ \frac{1}{2}&0&0&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}&0&0\end{matrix}\right)\]
E ela vai nos ajudar a fazer todo o resto. A utilidade de escrevê-la, além de ficar claro e bonitinho, é a seguinte: ela representa na linha $i$ e coluna $j$ as probabilidades de, estando na casa número $i$, ir à casa número $j$ em uma jogada. Se eu quiser a probabilidade de, estando na linha $i$, ir à coluna $j$ em duas jogadas, basta multiplicar a matriz $M$ por ela mesma! Aos que estão enferrujados em multiplicação de matrizes, eis a resposta:
\[{}\left(\begin{matrix}0&\frac{1}{2}&\frac{1}{2}&0\\ 0&0&\frac{1}{2}&\frac{1}{2}\\ \frac{1}{2}&0&0&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}&0&0\end{matrix}\right).\left(\begin{matrix}0&\frac{1}{2}&\frac{1}{2}&0\\ 0&0&\frac{1}{2}&\frac{1}{2}\\ \frac{1}{2}&0&0&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}&0&0\end{matrix}\right)=\left(\begin{matrix}\frac{1}{4}&0&\frac{1}{4}&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{4}&0&\frac{1}{4}\\ \frac{1}{4}&\frac{1}{2}&\frac{1}{4}&0\\ 0&\frac{1}{4}&\frac{1}{2}&\frac{1}{4}\end{matrix}\right){}\]
Ou seja, a chance de, estando na primeira casa, voltar a ela depois de duas jogadas é 1⁄4, a chance de estar na terceira casa depois de duas jogadas também é 1⁄4 e a chance de estar na quarta casa é ½. Mas o problema não é saber as chances de 2, 3, 10 ou 100 jogadas, queremos saber qual é a mais provável de cairmos em todo o decorrer da partida, o que é um problema diferente, mas que pode ser resolvido com essa matriz. Basta multiplicar essa matriz por ela mesma um número alto, bem alto de vezes, torcer para que ela comece a convergir para uma matriz razoável e dizer que essas serão as probabilidades em “tempo infinito”, ou seja, as chances de se estar naquelas casas depois de ter jogado muitas vezes.
Note, dizer que em um número alto de jogadas eu estarei mais provavelmente na casa X e dizer que terei passado várias vezes por X são afirmações bem diferentes, mas arrisco dizer que representam a mesma coisa, e o nome dessa afirmação é hipótese ergódica. Esse post não tem a menor pretensão de avançar nessas águas, que esse nome fique sendo, por enquanto, apenas um nome bonito para uma teoria.
Mas se elevar uma matriz ao quadrado é difícil, como elevar uma matriz a um número muito grande? Matematicamente falando, vamos elevar $M$ a $n$, o número de jogadas, e depois tomar o limite para $n\to\infty$, ou seja, vamos dizer que $n$ é um número muito, muito grande; o que, para Banco Imobiliário, consiste em uma excelente aproximação.
Parte geek do post, evite se não reconhecer a palavra “autovalor”. A parte rookie continua em seguida.
Os que já fizeram seu curso de álgebra linear conhecem a dica, vamos atrás dos autovalores dessa matriz e elevar esses caras a $ n$, depois mandar $ n$ para infinito e ver no que vai dar. Isso porque, felizmente, se escrevemos uma matriz como $M=UDU^{-1}$, onde $D$ é uma matriz diagonal, elevar $M$ a $n$ é escrever $ UDU^{-1}UDU^{-1}\ldots UDU^{-1}$ um número $ n$ de vezes, notando que os $ U^{-1}U$ do meio se cancelam, isso é o mesmo que $ UD^nU^{-1}$, e elevar uma matriz diagonal a uma potência é simplesmente elevar seus elementos a essa potência.
Posso me colocar várias perguntas como: “e se algum autovalor for maior que 1? A matriz vai explodir!” ou “E se todos forem menores que 1? A matriz vai para zero!” ou ainda: “E se algum for negativo? Como você eleva isso a infinito?!”; mas todas elas são sanadas quando invoco um corolário do poderoso teorema de Perron-Frobenius:
Teorema (de Perron-Frobenius): Entre outras coisas (esse teorema é bem poderoso), uma matriz estocástica como a do banco imobiliário possui o autovalor 1, único (não degenerado), e não há autovalores que, em módulo, sejam maiores que ele. O autovetor associado ao autovalor 1 possui todos os seus componentes de mesmo sinal. Em particular para matrizes como as do Banco Imobiliário, esse valor próprio 1 é o maior de todos os autovalores em módulo.
Eu poderia discutir bastante a razão desses resultados, já que Perron-Frobenius é um canivete suíço, adaptando-se a vários tipos de matrizes não-negativas diferentes. No caso da do Banco Imobiliário temos o fato importante de ser perfeitamente possível estar na casa $ i$ e voltar a ela mesma após um número $ m$ suficientemente grande de jogadas, e também ser possível voltar após $ m+1$ a essa mesma casa. Essa propriedade garante que 1 será o único autovalor de $ M$ no círculo unitário.
Esse corolário não deve surpreender ninguém, pois, se uma matriz estocástica vezes outra matriz estocástica continua uma matriz estocástica (eu teria que demonstrar isso, mas acredite em mim, é verdade), $ M^n$ deve também ser estocástica, então não pode ter autovalores maiores que 1 (que explodiriam se elevados a $ n\to\infty$), também não poderia ter apenas autovalores menores que 1, a matriz toda iria a zero quando elevada a $ n\to\infty$, não sobra tantas alternativas além do resultado de Perron-Frobenius. O que ele nos garante de interessante é a unicidade desse autovalor 1 e o sinal do autovetor associado.
E se você elevar todos os demais autovalores a $ n\to\infty$, eles logo logo vão para zero. Sobra o 1. Reconstruindo a matriz multiplicando por $ U$ e $ U^{-1}$, teremos uma surpresa, $ M^n$ com $ n\to\infty$ possui todas as linhas iguais, cujos componentes são os elementos do autovetor associado a 1. Essa surpresa é consequência da teoria ergódica, mas isso fica para outro post Dessa forma, o que queremos é esse autovetor associado ao autovalor 1.
Fim da parte geek.
O método descrito acima, se aplicado a nosso Banco Imobiliário Zona Leste, nos dará que a probabilidade de cair em todas as casas é a mesma, o que é esperado. Somos tentados a achar que no jogo do Banco Imobiliário ocorre o mesmo, mas esquecemos de elementos fundamentais da dinâmica do jogo, em particular da prisão, que muda tudo. Para explicar o efeito da prisão nas probabilidades das casas, introduzo um novo jogo, o Banco Imobiliário Zona Leste Deluxe:
Jogaremos usando um dado de seis faces. Nesse novo jogo, a matriz não será tão bonita quanto a anterior. A casa “Vá para a prisão” leva diretamente à prisão, quebrando a simetria do jogo e beneficiando as casas logo após a prisão, prejudicando aquelas que vêm antes. A matriz completa desse jogo será:
\[M=\left(\begin{matrix}0&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&0\\ 0&0&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}\\ \frac{1}{6}&0&0&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}\\ \frac{1}{6}&\frac{1}{6}&0&0&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}\\ \frac{1}{6}&\frac{1}{6}&\frac{1}{6}&0&0&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}\\ \frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&0&0&\frac{1}{6}&\frac{1}{6}\\ 0&0&1&0&0&0&0&0\\ \frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&0&0\end{matrix}\right)\]
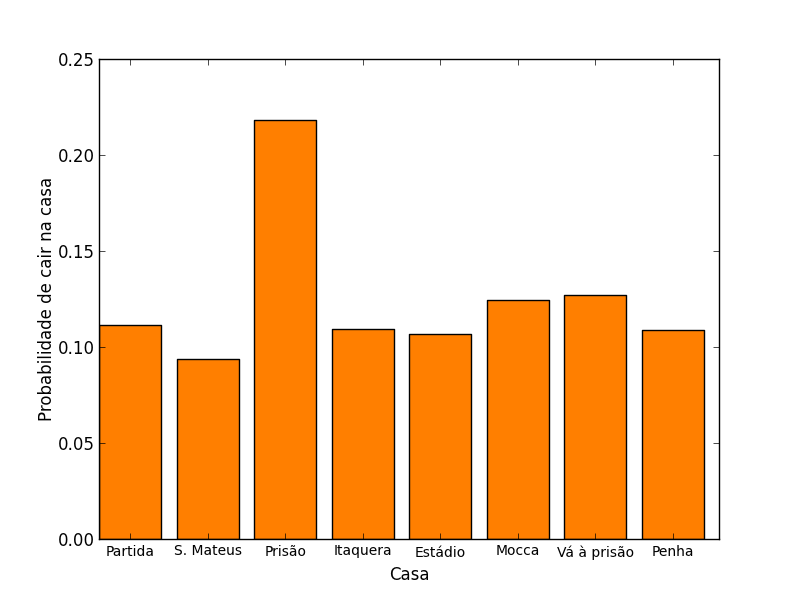
Aquela bela simetria da outra matriz já não mais existe, a prisão é a culpada, note a penúltima linha (representando a casa “Vá para a prisão”). Analisando quais serão as probabilidades de se cair em cada uma das casas após um grande número de jogadas usando a técnica da parte geek, ou seja, multiplicando a matriz por ela mesma muitas vezes, teremos:
O que é bem diferente de uma probabilidade uniforme, como no jogo anterior.
Apliquemos tudo isso ao verdadeiro Banco Imobiliário. Seu tabuleiro é mais completo, ele é jogado com dois dados e andamos a soma dos valores tirados, possui casas de sorte-ou-revés, diversas cores e muitas propriedades. Seu tabuleiro, a quem não se lembra, é:
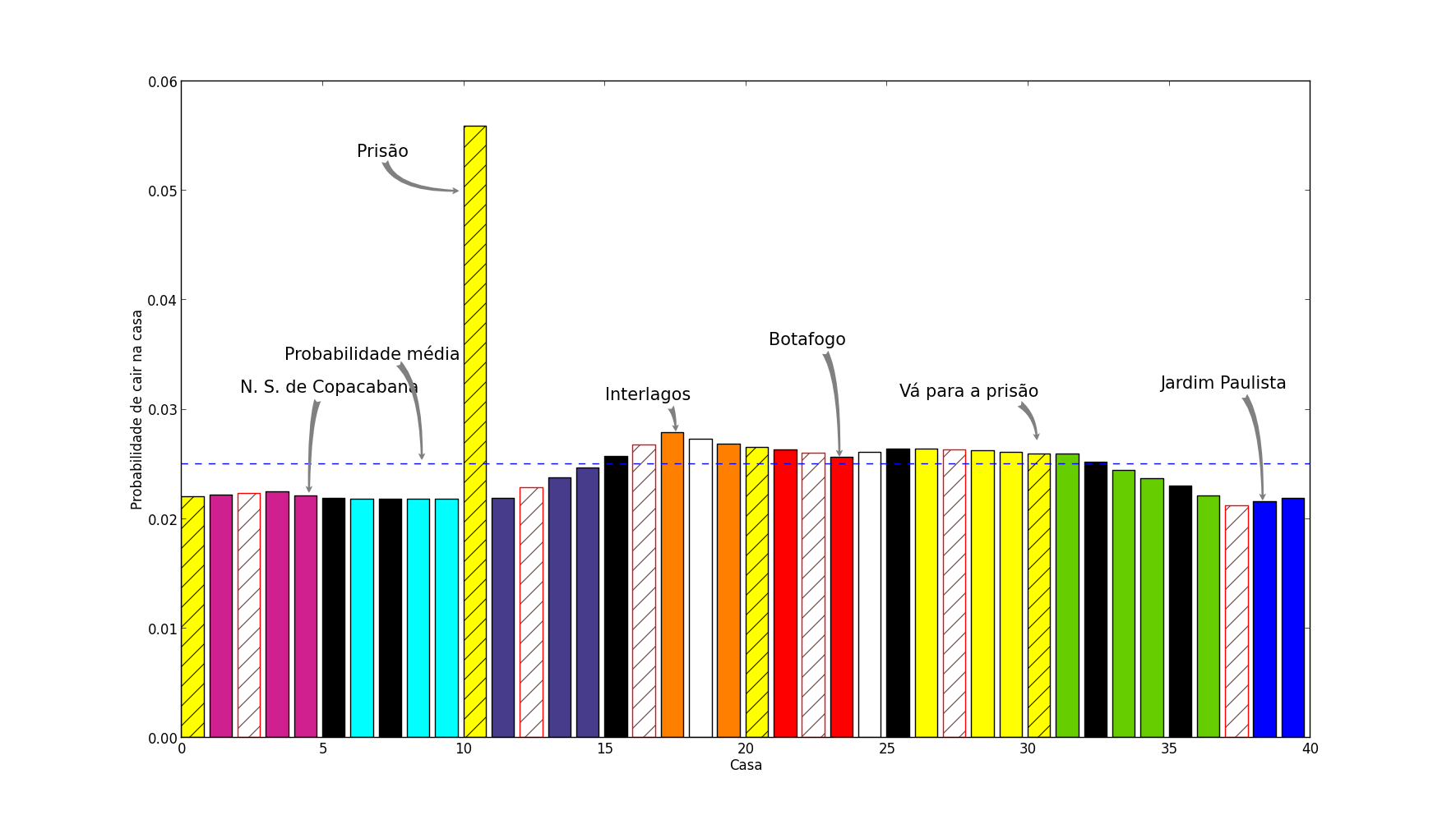
Não vou escrever sua matriz estocástica, não quero cuspir uma tabela de 40 linhas e 40 colunas nesse blog, mas acreditem, fiz as contas. A probabilidade de se encontrar em cada uma das casas é:
Levei também em conta a chance de 1/18 de se encontrar uma carta de ida à prisão nos espaços de sorte-ou-revés, foi o ajuste mais fino que fiz no modelo, para obter esses resultados. Ainda, ele não afeta em grande coisa a análise, pois as casas de sorte-ou-revés estão bem distribuídas no tabuleiro, apenas acentuam o efeito da prisão.
Notem que as casas rosa não são apenas as mais baratas e de pior rentabilidade, são também aquelas, juntamente com as azuis escuras, mais difíceis de atingir no tabuleiro. Interlagos e Morumbi, as tão desejadas laranjas, formam a dupla mais provável de casas para se atingir: são aquelas mais prováveis de encontrar após sair da prisão e, sendo a prisão a casa de longe mais provável, elas herdam um pouco dessa probabilidade.
Não jogo Banco Imobiliário há muito, entendo um pouco a razão. Podemos imaginar razões para a casa mais cara ser a mais provável, ou outras sutilezas descobertas na análise, mas isso é facilmente refutado pelo fato de países diferentes escolherem distribuições diferentes de valores de casa pelo tabuleiro; no jogo francês, a casa mais cara é a menos provável, substituindo o Jardim Paulista de nossa edição. Percebemos, por isso, que não é um jogo feito com tanto cuidado assim. Contudo, talvez se quando eu jogava soubesse um pouco mais sobre matrizes, mais sobre Frobenius, tivesse mais sorte no dado, talvez assim eu tivesse gostado, jogado, ganhado, ou, quem sabe, até mesmo terminado uma partida de Banco Imobiliário.


Ótimo post. Cada vez gosto mais de estatística. Sou aluno do terceiro ano do ensino médio, e finalmente comecei a ver um sentido em matrizes (não que eu tenha lido algo além do primeiro parágrafo da parte geek).
Nossa! Mt interessante! Mt claro e bem escrito! Msm p qm n lembrava da existencia de um tal frobenius 😉
Muito legal também ver como todos (ou pelo menos alguns) os caminhos levam a Roma! Sei muito pouco de álgebra e nunca ouvi falar do teorema de Perron-Frobenius, mas o que eu sei de estatística me faz ver que o seu procedimento é essencialmente o mesmo que achar a distribuição estacionária de uma cadeia de Markov!
Legal saber também que entre as casas baratas as vermelhas podem ser uma boa pedida. Vou prestar mais atenção nelas da próxima vez que jogar.
O procedimento é exatamente esse, eu associo a cadeia de Markov a uma matriz estocástica e busco o estado de equilíbrio dela, o vetor de probabilidades x tal que Mx=x. Isso equivale a buscar o autovetor do autovalor 1, usei o Perron-Frobenius para garantir que existe esse estado de equilíbrio.
Olá Ricardo, tudo bem?
Estava lendo o seu post e me surgiu uma dúvida: você supôs que essa matriz é diagonalizável para resolver o problema. O que garante que isso é verdade sempre para uma matriz desse tipo? Não encontrei nenhum jeito “simples” de ver isso.
De qualquer maneira, achei genial o post.
Excelente pergunta, você percebeu que eu tentei te enganar! Para evitar um comentário mais denso, eu tratei de forma ad hoc essa matriz como diagonalizável. Ela é, mas só porque eu mandei o computador diagonalizar e ele conseguiu, mas não necessariamente precisaria ser. Contudo, em um jogo de Banco Imobiliário em que nenhuma casa é de impossível acesso e nenhuma casa é uma prisão eterna (ou seja, a matriz associada é irredutível), Perron-Frobenius me garante: elevar essa matriz a N e tomar N para infinito fará a matriz convergir para uma cujas linhas são o autovetor associado ao autovalor 1.
Eu disse que o autovetor associado ao 1 será a probabilidade de cair em cada casa, e esse comentário anterior faz entender a razão. Aqui você acha a propriedade 5., que é válida para matrizes não-negativas irredutíveis, e no caso de matrizes estocásticas teremos que o autovetor à esquerda será o vetor constante igual a 1. Como k também será 1, você percebe que a matriz tende a se tornar o autovetor associado ao 1 repetido em todas as linhas.
No jogo, o que isso significa? Se a matriz estocástica tem como interpretação “estou na casa i qual a chance de ir para j” e elevar a uma potência N consiste a acrescentar a frase “depois de N rodadas”, o teorema de Perron-Frobenius nos diz que se nenhuma casa é inacessível e nenhuma é uma prisão eterna, jogadas vezes o suficiente, você não tem mais como saber de qual casa partiu! Assim, todas as linhas devem ser iguais!
Resumindo: não garanto que é diagonalizável, mas não preciso disso para aplicar Perron-Frobenius e extrair o autovalor 1 e o autovetor associado.
Muito obrigado, esclareceu muito!! Perron–Frobenius é realmente muito poderoso! Tinha pensado na mesma interpretação final do resultado, e achei realmente espantoso que desse tão certo!
Parabéns pelo seu blog! Esse é um dos meus posts favoritos!
Muito legal a análise sobre o jogo!
Compartilho desta busca pela tática ótima de se jogar qualquer jogo de tabuleiro.
Convido-o a conhecer o Settlers of Catan – jogo que fará a cabeça explodir!
Saudações!
Olá Ricardo você possui algum arquivo o qual apresenta as passagens matemáticas, as quais apresentastes na parte geek.Gostaria de entender de uma forma mais detalhada esta estratégia.
Excelente post.
Fico feliz que tenha gostado! Infelizmente não tenho isso em um arquivo detalhado com passagens e tal, mas tenho certeza de que você encontra o método, especialmente o uso de Perron-Frobenius, em um bom livro de processos de Markov.
Gostaria de comprar um Bco imobiliária igual a esse como faço
Banco Imobiliário Zona Leste Deluxe é infelizmente um produto sem muita demanda, não partimos para a produção industrial dele ainda.