Arquivo mensais:setembro 2012

Quase arte

Rookie

Se você, como eu, possui um leve TOC com simetrias, gosta das coisas em seus devidos lugares, detesta paredes não-perpendiculares pelo dilema de ter que escolher um eixo para alinhar coisas na sala ou, jogando Carcassonne, passa mais tempo arrumando as peças que pensando em sua jogada, esse post não é para você.

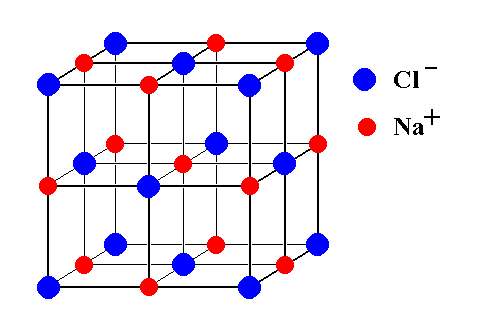
Quando eu era mais novo, passei por uma fase “física dos materiais” e me interessei bastante por propriedades eletrônicas de sólidos e cristais. Aprendemos que cristais são agregados de átomos em um padrão que se repete, que se reproduz. Um cristal de sódio e cloro, por exemplo, agrupa-se em uma estrutura periódica cúbica que se repete muitas, muitas vezes até formar um conglomerado colossal de átomos, que chamamos de sal.

Nessa aula de cristais, aprendi que toda estrutura cristalina possui um motif, cuja tradução desconheço. Essa palavra não é exclusiva da física ou da matemática, motif é, grosso modo, um fragmento que comporá uma grande obra, como um tijolo compõe casas. A quinta de Beethoven talvez possua o motif musical mais conhecido, as famosas três notas curtas acompanhadas de uma longa que abrem a sinfonia. Nos cristais é o mesmo, vejamos o motif do sal de cozinha:

Sendo a construção de um cristal feita com a repetição indefinida desse motif. Não apenas nos cristais, encontramos problemas similares a esse quando tentamos comprar azulejo para nossa casa. Durante muito, acreditou-se que redes cristalinas pudessem ser apenas de um entre dezessete tipos, conhecidos como os grupos de papéis de parede. Se você tem um azulejo em sua casa, garanto que ele pertence a um desses dezessete grupos.

Mas note que todas essas redes regulares possuem algo em comum: uma simetria. Redes triangulares possuem simetria de rotações por 120°, as quadradas são invariante por rotações de 90° e as hexagonais, por rotações de 60°. Essas simetrias são características dos cristais e uma boa parte de nossas técnicas de medição consiste em medir essa simetria, da seguinte ideia: você lança luz no cristal (ou elétrons, o importante é lançar algo), veja como o cristal rebate a luz e estuda o perfil formado na saída da luz. Com esse perfil, você entende como o cristal funciona. Um cristal de alumínio possui, por exemplo, simetria hexagonal. Não por menos, seu padrão de difração é algo assim:

No entanto, em 1982, Dan Shechtman faria medições de um composto de alumínio e manganês que lhe daria o seguinte padrão de difração:

diffraction

É difícil entender o quanto esse padrão chocou Shechtman, e como escandalizaria a comunidade da cristalografia. Se o padrão do alumínio era um hexágono, o que é perfeitamente aceitável, esse é um decágono. Em alguns pontos, traçando as linhas certas, percebemos uma simetria pentagonal no desenho. O problema é exatamente esse: a simetria pentagonal (72°) é proibida aos cristais! Você consegue criar um tapete usando quadrados, triângulos e hexágonos, mas jamais pentágonos! Você pode se enganar enfiando um pentágono aqui e ali, mas isso será apenas usar um pentágono para compor seu motif, e esse motif será reproduzido de forma triangular, quadrada ou hexagonal. Shechtman havia descoberto um monstro.

Com medo de sua descoberta, Shechtman levou dois anos para tomar coragem e publicar seus resultados. A comunidade científica estranhou de início, mas a matemática do assunto já havia sido desenvolvida desde 1964, estávamos vendo o primeiro caso de um quasicristal. Apresento-lhes um padrão similar ao do composto estudado por Shechtman, o belíssimo Al-Pd-Mn:

Notem a ausência de um padrão claro de repetição, um motif, e, ainda, uma aparente simetria que se quebra em pontos para ceder a outra simetria em uma dança de padrões pentagonais. Átomos de fato se agrupam assim, por uma razão atomicamente simples: muitas vezes, os compostos desejam fazer cinco ligações eletrônicas, que se repelem mutuamente. Nesse jogo de repulsão, elas forçam um padrão pentagonal e, quando ele não é mais possível (porque não há como cobrir um solo com pentágonos), há a quebra de simetria.

Esse tipo de padrão, ou de quase padrão, não é muito comum em nossa sociedade e nossa arte, mas a história é bem diferente na arte islâmica. Não sou especialista, mas sei que o número cinco não é lá bem visto nas religiões que herdamos, em especial o pentágono ou a estrela de cinco pontas. No mundo árabe, o cinco é um número querido, há cinco orações por dia, cinco meses sagrados no ano, e, em particular, o pentágono ou a estrela não apresentam problema. Não de forma surpreendente, encontramos na arte islâmica criada no período de ouro das civilizações árabes exemplos vastos de quasicristais:

Santuário de Darb-i Imam, em Isfahan

Igualmente interessantes são as propriedades de repetição dos quasicristais. Ainda que eles não possuam motif, possuem regiões que se repetem com alguma frequência. De fato, podemos afirmar que, grosso modo, toda região de diâmetro $R$ se repete em até uma distância de $2R$. Como exemplo, note que essas regiões pentagonais verdes assinaladas se repetem em uma distância ainda menor que seu tamanho:

Mais que isso, as diversas regiões assinaladas demonstram todas uma repetição em algum ponto próximo, dependendo do tamanho da região considerada, nunca estando mais que o dobro de seu tamanho de distância de seu irmão gêmeo mais próximo.

Muitos outros compostos foram descobertos com padrões desse tipo, e suas propriedades e aplicações ainda são um terreno aberto. Infelizmente me desviei desse campo, matrizes me atraem mais que pentágonos, mas não deixo de apreciar esses padrões, quase perfeitos, quase simétricos e totalmente belos.

7 respostas

O princípio do pombal

Rookie

Em física e matemática, é bem comum encontrarmos princípios que parecem óbvios com consequências complicadas. Meu exemplo favorito é a relação conhecida como equação mestra na física estatística que, se lida em português, seria: “o quanto variou é o quanto entrou menos o quanto saiu”. Por mais evidente que isso seja, essa equação toma formas cabulosas em situações não muito complicadas e exige bastante suor para ser resolvida.

Mas o assunto de hoje não é a equação mestra, mas outro princípio, talvez ainda mais simples: o princípio da casa dos pombos, ou princípio do pombal.

Princípio da casa dos pombos: se há mais pombos que casas em um pombal, alguma casa terá mais de um pombo.

Eis uma aplicação desse princípio:

E por mais óbvio que ele pareça, não é nada inútil se lembrar dele como técnica de demonstração de resultados bem interessantes. Um deles, meu favorito, é uma espécie de jogo com sequências. Para ilustrar, imagine uma rua com $n$ casas. Cada casa deve possuir um número, e você pode escolher o número que quiser. Eu afirmo que existe um grupo de casas vizinhas cujos números, somados, resultam em um múltiplo de $n$.

Vejamos um exemplo. Imagine treze casas que possuem os seguintes números: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 e 14. Se houvesse uma casa com o número 13, ela seria sozinha o múltiplo de 13 que quero, isso não me serve de muita coisa. Note que, nessa rua, temos os vizinhos 5, 6, 7 e 8, e 5+6+7+8=26, que é um múltiplo de 13.

Mas podemos pegar sequências mais complicadas, como, por exemplo, um antigo telefone meu: 41921561. Eu tenho certeza absoluta de que existem números vizinhos que, somados, resultam em um múltiplo de oito (que é o tamanho da sequência). Basta caçar um pouco para encontrar que 4+1+9+2=16.

Ou, ainda, tomemos essa permutação de meu RG: 158313734. Cacemos os vizinhos que somados dão um múltiplo de nove, e uma leve busca nos leva a 5+8+3+1+3+7=27. Você certamente pode encontrar combinações mais simples, eu não disse que era única, apenas que existe.

Esse resultado, que é um divertido jogo quando se está profundamente entediado em uma sala de espera ou durante uma viagem de trem, é provado com o princípio do pombal. Para tal, tome sua sequência de tamanho $n$, da forma $a_1,a_2,\ldots a_n$. Pense agora em todas as possíveis sequências com a mesma ordem dessa sua original que começam no $a_1$, ou seja, as sequências:

\[a_1\]

\[a_1,a_2\]

\[a_1,a_2,a_3\]

E assim por diante. Pense agora na soma dos elementos delas. Se alguma dessas somas já dá um múltiplo de $n$, nosso problema está resolvido, então vamos supor o pior dos casos, nenhuma delas é um múltiplo de $n$. Assim, a soma dessas sequências, dividida por $n$, deve dar algum resto, e haverá $n-1$ possibilidades de resto.

Ainda em um exemplo, se minha sequência possuísse quatro elementos, as somas dessas subsequências teriam que ter resto ou 1, ou 2, ou 3. Se o resto fosse zero, seria divisível.

Como você tem $n$ sequências possíveis e apenas $n-1$ restos possíveis, então, pelo princípio do pombal, terá, necessariamente, duas sequências diferentes cuja soma tem o mesmo resto na divisão por $n$. Ora, subtraia uma da outra que você terá uma sequência de vizinhos cuja soma, dividida por $n$, possui resto zero, logo, é divisível!

Para entender melhor, vou aplicar esse raciocínio a uma sequência específica: 1 2 1 3 6. As subsequências possíveis são 1, 1 2, 1 2 1, 1 2 1 3 e 1 2 1 3 6. Suas somas serão, respectivamente, 1, 3, 4, 7 e 13. Note que, dividindo por 5, esses números produzem respectivamente resto 1, 3, 4, 2 e 3. A segunda e a última sequência possuem o mesmo resto! Então tirando a segunda da última teremos os elementos 1 3 6 que, somados, dão 10, um múltiplo de 5.

Não sei se ficou claro, na verdade, acho que ficou confuso, mas vou deixar assim enquanto não encontro maneira melhor de escrever. Provar o princípio do pombal, no entanto, me parece mais difícil que esse resultado que acabei de enunciar, talvez usando algum resultado dessa parte mais fundamental de teoria dos conjuntos, propriedades com bijeções, injeções e sobrejeções, a noção de cardinalidade, teria que pensar um pouco. Por enquanto, fica o resultado das sequências, das casas, e a demonstração dos pombos.

2 respostas

Fogo e chama

Rookie

Um dia desses, tive vontade de escrever um post sobre o fogo. Sempre fui fascinado pela chama, o brilho, o calor, seu movimento. Não conseguiria, contudo, escrever nada mais didático que esses dois vídeos combinados:

[youtube http://www.youtube.com/watch?v=5ymAXKXhvHI]

[youtube http://www.youtube.com/watch?v=ITpDrdtGAmo]

Enjoy.

Deixe um comentário

Coleção completa

Geek

Quando era criança, fui atingido pela mania dos tazos da Elma Chips como todos os meus colegas. Abria o salgadinho antes mesmo de chegar à aula, longe ainda do recreio, e recolhia o precioso prêmio do pacote: um disco plástico que servia de moeda de aposta e demonstração de habilidade no intervalo. Eu não era muito bom nisso, e não tinha tantos amigos, então minha principal fonte de Tazos eram o fandangos.

Via colegas com tubos repletos de tazos, coleções completas, era invadido por essa inveja e, talvez mais, por uma pergunta séria: como aquilo era possível? Eu colecionava havia meses e não chegara perto da metade da coleção, possuía muitos repetidos e aquele do Papa-Léguas era mais difícil de encontrar que filhote de pomba. Não imaginava como aquilo era possível, culpava os pais do garoto sortudo, deviam ter comprado caminhões de baconzitos, e, no fundo, queria saber: de quantos fandangos eu precisaria para completar minha coleção?

Essa pergunta está mal-feita, vamos melhorá-la. Mais interessante seria perguntar: qual o número médio, o valor esperado, de salgadinhos que preciso comprar para completar minha coleção? Em outras palavras, a partir de qual número de fandangos é mais provável que eu já tenha a coleção completa que o contrário? E, como pergunta bônus, quão improvável se torna, a partir desse número, não obter os preciosos tazos?

Havia tazos mais raros, é verdade, mas a pergunta já está bem difícil, então tomo como hipótese que a chance de tirar qualquer um dos tazos é a mesma. E para continuar, precisamos primeiro saber quantos são eles, e eis a coleção toda:

Se você está interessado na resposta, mas não conhece tanto de probabilidade, o que segue não será tão interessante (vou fazer as contas, é o que faço da vida, não consigo evitar). Mas você pode pular para o final do post e ver as conclusões sem culpa, se confiar em mim. Se, no entanto, você entende de probabilidade, jamais confie em mim. Suponha que eu já tenha $ k$ tazos diferentes, sendo $ n$ possíveis, a chance de eu tirar um repetido é $ \frac{k}{n}$. Assim, a probabilidade de eu precisar de exatamente $ s$ salgadinhos para tirar um diferente é $ \left(\frac{k}{n}\right)^{s-1} \left(1-\frac{k}{n}\right)$, que é uma parte a chance de eu tirar $ s-1$ repetidos e outra parte, no $ s$-ésimo salgadinho, tirar um diferente. Essa é $ P(s)$, a chance de eu precisar de $ s$ fandangos para tirar meu tazo diferente. Para calcular o valor esperado de salgadinhos até o próximo tazo diferente, ou seja, de $ s$, basta tomar:

\[ \sum_{s\geq 0}P(s).s=\sum_{s\geq 0}\left(\frac{k}{n}\right)^{s-1}\left(1-\frac{k}{n}\right).s=\frac{1}{1-\frac{k}{n}}\]

Essa última passagem fiz na malandragem, vale a pena explicar. Vou chamar $ \frac{k}{n}$ de $ x$ porque digitar essas coisas no WordPress cansa. Vou aplicar a distributiva, manobrar os índices e converter tudo em uma progressão geométrica de soma bem fácil:

\[\sum_{s\geq 0}x^{s-1}\left(1-x)\right).s=\sum_{s\geq 0}x^{s-1}s-\sum_{s\geq 1}x^s.s=\sum_{s\geq 0}x^s(s+1)-\sum_{s\geq 0}x^s.s=\sum_{s\geq 0}x^s=\frac{1}{1-x}\]

Então o número esperado de salgadinhos que devo comprar é a soma dos salgadinhos esperados para cada tazo que vou tirando, ou seja:

\[ \sum_{k=0}^{n-1}\frac{1}{1-\frac{k}{n}}=\frac{n}{n}+\frac{n}{n-1}+\ldots+\frac{n}{2}+\frac{n}{1}\]

Sem magia até agora, eu apenas expandi a série. Eu poderia calcular exatamente esse valor para $ n=80$, mas gosto de resultados mais gerais, e noto que essa soma é $ n$ vezes a série harmônica. Ela diverge, e não é surpreendente que eu precise de infinitos fandangos para tirar infinitos tazos, mas felizmente conhecemos razoavelmente bem o comportamento dessa série. O número esperado de salgadinhos necessários para completar uma coleção de $ n$ tazos é, portanto, $ nH_n$, onde $ H_n$ é o n-ésimo número harmônico. Para $ n$ grande, podemos usar a aproximação $ H_n\approx \log n+\gamma$, onde $ \gamma$ é a constante de Euler-Mascheroni (aproximadamente 0,5772).

Chegamos ao valor $ 80*(\log(80)+\gamma)=396,74$, certamente aproximado. Esse é o número médio de vezes que crianças completam suas coleções. Temos a média, a próxima pergunta é: quão provável é estar longe da média? Ao invés de tentar calcular com manobras intrincadas as flutuações desse número em torno da média, tomarei, a princípio, o exemplo de cinco crianças: Aline, Bruno, Carlos, Daphny e Eduardo. Eles começam suas coleções juntos e têm poucos amigos, logo, contam apenas com os salgadinhos para obter os preciosos discos. Eis uma simulação que fiz do resultado da coleção dessas cinco crianças:

Notamos algumas coisas interessantes. Primeiro, teremos que gastar aproximadamente metade dos salgadinhos totais necessários apenas para conseguir os dez últimos tazos; a matemática é cruel com coleções quase completas. Segundo, o valor necessário para completar é muito diferente nos cinco casos, isso exige um estudo mais sério.

Para tal, calibramos o computador para simular a coleção de tazos, ou o álbum de figurinhas (o problema é o mesmo) de 20.000 crianças. Fiz um histograma com a quantidade de salgadinhos necessária para completar toda a coleção e a porcentagem das crianças simuladas que precisaram daquela quantidade de salgadinhos para obterem o último tazo.

Notamos a larga variância dessa distribuição: haverá um grande número de crianças sortudas e um grande número de azaradas! Confirmamos o valor esperado, 396 parece de fato uma boa média dessa distribuição, e confirmamos o quão sórdido é o raciocínio da Elma Chips: algumas crianças precisariam de 900 salgadinhos para terem a coleção completa!

Contudo, esse modelo não representa bem a realidade, talvez apenas a minha, mas a maior parte das crianças tinha como maior objetivo as trocas de tazos, as disputas, completar a coleção contando com o salgadinho dos outros. Eu mesmo consegui dois amigos para fazer uma sociedade, ainda que cada um quisesse, para si, uma coleção completa. E esse será meu modelo de trocas: os amigos são amigos perfeitos, todo tazo repetido é compartilhado e o objetivo maior é, para $ y$ amigos, formar $ y$ coleções completas.

De forma não surpreendente, o número de fandangos que cada criança deve comprar reduz drasticamente com as trocas. Se ele antes precisava gastar quase um ano de lanches de salgadinho para encontrar os dez últimos, esses famigerados dez podem ter sido encontrados por algum colega que já até o tirou uma vez. Simulei o resultado com grupos de 1, 5, 10 e 30 crianças, sendo os resultados no histograma abaixo:

Esses valores são quantos fandangos cada um precisará comprar, ou seja, no grupo de dez, se dez amigos precisaram de 2000 fandangos para fechar a conta, contabilizo 200 para cada criança. Os valores médios de salgadinhos individuais obtidos para 1, 5, 10 e 30 são, respectivamente e aproximadamente, 398, 194, 154 e 120. Fiquei curioso para estudar a convergência dessa série, se vai para algum lugar (certamente converge, sendo decrescente e limitada em 80) e se esse lugar é 80, uma utopia em que todas as crianças do país montam suas coleções juntas; mas esse post já está longo e tanto salgadinho não deve fazer bem a esses meninos.

Por fim, noto que a amizade é o melhor investimento, você pode, em poucos meses de lanche, completar sua coleção de tazos ou figurinhas se encontrar, em uma sala de aula, trinta amigos perfeitos. A probabilidade desse fato, no entanto, mesmo em um modelo bem otimista, é extremamente baixa.

2 respostas