Hoje falamos de álgebra, mas não aquela álgebra linear, coisa séria, de gente grande. Comento com vocês um resultado interessante e bonito da teoria de grupos, chamado teorema de Lagrange. E antes de enunciá-lo, apresento seus elementos, vamos conversar sobre o que é um grupo.

A definição formal não é difícil, mas prefiro definir com palavras a símbolos. Um grupo é um conjunto de elementos que podem ser “somados”, não importando muito o que essa ideia de soma seja. É importante que haja um elemento do conjunto “eleito” como o elemento neutro, aquele que, somado a qualquer um, não afeta esse qualquer um. Na soma convencional, ele é o zero. Na multiplicação, ele é um 1. Nas multiplicação de matrizes, é a identidade. Também é importante que você, tendo somado um elemento, sejá capaz de “subtrai-lo”, ou seja, realizar a operação inversa. Na soma tradicional, o inverso de $a$ é $-a$, na multiplicação, é $1/a$. Nas matrizes, teremos a matriz inversa, o que nos prova que as matrizes não formam um grupo na multiplicação delas. Por fim, queremos que o conjunto seja fechado, ou seja, é impossível, com somas de gente do conjunto, obter alguém de fora dele.

Exemplos de grupos são fáceis de se encontrar: os inteiros com a operação soma, os reais sem o zero com a operação vezes, o conjunto de matrizes quadradas inversíveis de ordem n e os conjuntos de restos de divisão. Esse último merece alguma atenção, pois não só tem aplicações interessantes como é crucial em algumas áreas dessa matéria.

Ao fazer uma divisão por, digamos, 5, temos cinco opções como resto, 0, 1, 2, 3 e 4. Se um número dividido por 5 deixa resto 3 e outro número deixa resto 3, a soma deles deixará resto 1, essa será a regra de nosso grupo “resto de 5”, denotado $\mathbb{Z}/5\mathbb{Z}$. É como se você somasse números normalmente e, a cada vez que eles passam 5, você tira 5 do número. Nesse grupo, 1+1=2, 2+2=4 e 3+3=1. É fácil ver que todos possuem inverso, sendo, por exemplo, o inverso de 3 o número 2, o inverso de 4 o número 1 e assim por diante. Em particular, ele é um grupo finito, e por isso gosto dele. Neste post, vou falar apenas de grupos finitos, eles já atingem uma complexidade suficiente para deixar qualquer matemático feliz.

Se você acha o grupo descrito acima artificial, veja seu relógio. Ele é o grupo $\mathbb{Z}/24\mathbb{Z}$, pois 3+3=6, 6+6=12, mas 12+12=0, somar doze horas ao meio-dia não é ir à hora vinte e quatro, é voltar à meia-noite, hora zero.

E se falamos de grupos, podemos falar de subgrupos. Algum subconjunto de nosso grupo pode ser, em si só, um grupo. No caso do relógio, os elementos 0, 3, 6, 9, 12, 15, 18 e 21 formam um subgrupo. Eles herdam a operação do grupo original e operados entre si continuam entre si, não há como você, somando esses horários, atingir um horário que não esteja nessa lista. O grupo total possui 24 elementos, e esse subgrupo possui 8 elementos. E o que o teorema de Lagrange nos diz é isso:

Teorema (de Lagrange): O número de elementos de um subgrupo de um grupo finito é sempre um divisor do número total de elementos do grupo.

No nosso caso, teremos que 8 é um divisor de 24. Como consequência, podemos perceber que todo grupo que possui um número primo de elementos não possui subgrupo que não seja ou ele mesmo, ou um subgrupo composto apenas pela identidade. Por mais elaborada que seja a construção de seu grupo, se ele possui 11 elementos, não possui nenhum subconjunto que em si seja um grupo, e esse é um resultado bem divertido.

A prova desse teorema não é tão trivial para quem começou agora a ver grupos, então dou apenas uma ideia da demonstração. Se $G$ é um grupo finito e $H \subset G$ é também um grupo com a mesma operação, logo é um subgrupo, então vamos chamar os elementos de $H$ de $h, h_2, h_3\ldots$. Se $H=G$, o teorema está provado para esse caso, então vamos supor que $H \neq G$, tomemos um $g\in G$ que não está em $H$. Note que se $g\not\in H$, então a operação de $g$ com qualquer elemento de $H$ também não está em $H$. Por quê?

Sabemos que $H$ é um grupo, então todos lá possuem inverso. Se $gh_i = h_j$, poderíamos operar os dois lados da equação com $h_i^{-1}$ pela direita e obter $g = h_jh_i^{-1}$. Se escrevemos $g$ como uma composição de elementos de $H$, ele tem que estar em $H$, o que é absurdo por hipótese.

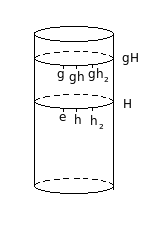
Intuitivamente, a ideia é pensar em $G$ como um cilindro e $H$ como um disco desse cilindro, como essa figura mostra:

O subgrupo $H$ gera, para cada elemento que não pertence a si, todo um anel novo de elementos, apesar de eu hesitar em chamar isso de anel porque, em álgebra, esse nome já é usado para outra coisa, então prefiro chamar de círculo. Ora, dá pra perceber que todo elemento de $G$ pertencerá ou a $H$ ou a um desses círculos formados por $H$. Todos os círculos possuem a mesma quantidade de elementos (pois se $gh_i = gh_j$, podemos cortar $g$ dos dois lados e provar que $h_i = h_j$), logo, o número total de elementos de $G$ deve ser um múltiplo do número de elementos de $H$.

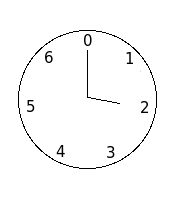
Esse teorema é um jeito de interessante de entender a razão de nossas horas serem contadas em 12 ou 24, esses números possuem muitos divisores! Como se houvesse um corolário do relógio cruel: não são feitos relógios com um número primo de horas, como, por exemplo, esse relógio cruel:

Nesse caso, nenhuma hora inteira seria sensata para se prescrever um medicamento, pois todas elas atravessariam todo o relógio antes de voltar para a mesma hora. Em outras palavras, percorrer este relógio de duas em duas, três em três ou quatro de quatro horas atravessará todo o relógio antes de repetir a primeira hora, pois o número de elementos de qualquer subgrupo deve ser um divisor do número de elementos do grupo. Isso faria o paciente acordar em todas as horas inteiras que deveria estar dormindo, e o mesmo aconteceria se, em nossos relógios, um médico receitasse um comprimido de sete em sete horas. Pode parecer uma aplicação estúpida, mas não é; o fato de nossa divisão do dia em vinte e quatro horas tem como razão histórica a grande quantidade de divisores que possui.

Você certamente pode chegar a essa mesma conclusão usando propriedades elementares de MMC e MDC, mas essa visão, mais abrangente dos grupos finitos, é capaz de nos levar a abstrações mais profundas e a grupos mais complexos, alguns nem numéricos, mas este resultado ainda vale. Muita coisa é grupo, e, em todos os finitos, vale o teorema de Lagrange.