Esses dias, saiu o resultado do prêmio Abel 2012! Se a matemática tivesse um Nobel, seria o prêmio Abel. Em muitos sentidos, ele me parece mais justo que a medalha Fields, que é atribuída apenas a matemáticos cuja idade é menor que 40 anos e, dessa forma, ignora avanços matemáticos dos mais experientes. Muitos vão dizer que matemático bom é matemático novo, gosto de lembrar que Weierstrass demonstrou o teorema que leva seu nome quando já passava dos 70, mas esse debate vai longe.

E o ganhador foi Endre Szemerédi, um matemático que trabalha na área de combinatória extrema. É uma área de demonstrações elementares e complicadas, e com elementar eu quero dizer “que não se apoia em resultados sofisticados”, ou seja, bastante coisa é demonstrada na raça e todas as provas acabam saindo bem elaboradas. Caracterizar a área é mais fácil com exemplos, e o melhor deles é o próprio teorema de Szemerédi, cujo tipo de pergunta que ele se dispõe a responder é: dados todos os números de 1 a 10.000, quantas números eu posso escolher antes de, com eles, poder formar uma progressão aritmética de tamanho $k$?

E essa pergunta não é fácil, pois a escolha de uma trinca pode atrapalhar a escolha de outras. Para entender a pergunta com mais cuidado, é mais fácil pensar em um jogo. Eu tomo os números de 1 a 100, por exemplo, e você pode ir escolhendo números. O desafio é: quantos você consegue escolher antes de, com os que você escolheu, formar uma P.A. de três elementos? Digamos que você escolha o 1 e o 2, já não pode escolher o três. Se escolher o 4 e o 6, não pode mais escolher o 8, e assim por diante. Esse tipo de problema, da classe de combinatória extrema, é tratado pelo teorema de Szemerédi.

Ele não te conta quantas exatamente você pode formar, ele vai além, com um resultado bonitinho. Se você está interessado em não formar progressões aritméticas de tamanho $k$ (no exemplo do jogo $k=3$), e deve tomar números de 1 a $n$ (que no exemplo foi 10.000, depois 100), eis o que o teorema de Szemerédi vai te contar: dado o jogo descrito acima, com você querendo evitar progressões aritméticas de tamanho $k$, eu sempre posso escolher um $n$ suficientemente grande para que você, ainda que seja o melhor jogador do mundo nisso, não possa escolher mais que 1%, ou 0,1% dos números disponíveis, ou 0,001%, eu posso, aumentando o $n$, estabelecer uma porcentagem tão pequena quanto eu quiser dos números disponíveis para você escolher.

Pensando um pouco, quanto maior for o intervalo de números possíveis, maior é o número de razões possíveis para a P.A., mas esse resultado não é intuitivo e é, aliás, bem divertido, eu posso tomar um $n$ tão grande a ponto de deixar uma fração de $10^{-23}$ desses números possível de ser escolhida, mesmo que você use a melhor tática possível de escolha de números.

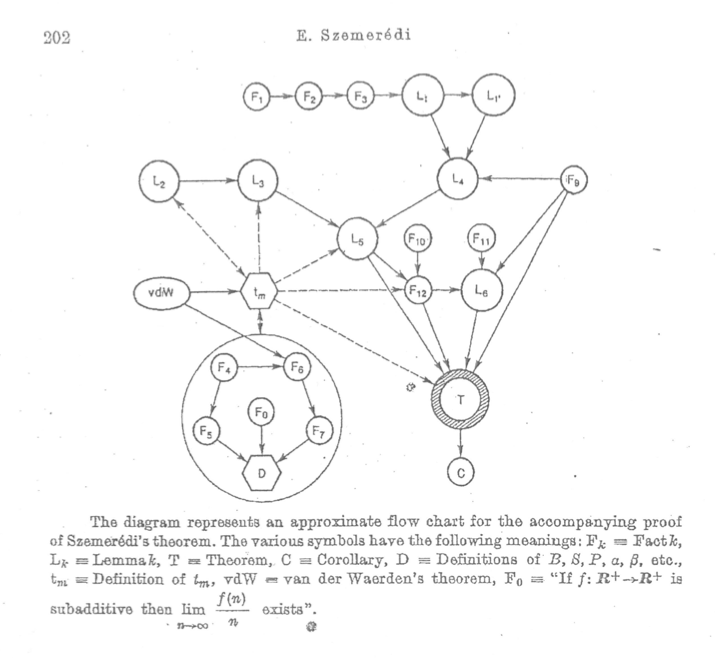
Falar em aplicações desse teorema é algo um pouco mais complicado, deixo para esse belo texto a respeito. Mais interessante que isso é tentar olhar de relance as engrenagens da demonstração, que é uma das mais sofisticadas que já vi. Enquanto muitos teoremas matemáticos possuem uma “linha direta” de demonstração (exemplo: cobre com abertos, tira uma subcobertura finita, prova que existe uma bola aberta centrada no ponto que não toca na cobertura, e você provou que todo espaço métrico compacto é fechado), o teorema de Szemerédi precisa de um diagrama para você entender o caminho que ele fez e, somente esse diagrama, já parece a penúltima fase do Metroid de Super Nintendo.

Você começa dos primeiros fatos (F’s), atravessa os lemas (L’s) e vai provando flecha por flecha até reunir ferramentas o suficiente para provar o T, o teorema de Szemerédi. Essa demonstração ganhou um espaço no meu coração apenas pelo pequeno carrossel no diagrama. E esse teorema possui aplicações também pelos resultados intermediários que demonstra, em especial o lema de regularidade de Szemerédi, usado para diversos outros resultados. E se não conseguimos contemplar completamente o poder e as aplicações desse teorema, ao menos apreciemos o intrincado jogo de demonstrações de sua prova que é, muito justamente, digno de um dos maiores matemáticos vivos da atualidade.