A natureza dificilmente gosta de ajudar o cientista. No ensino médio, aprendemos física em um mundo bem idealizado, sem atrito nas superfícies, sem resistência do ar e sem muito compromisso com a realidade. Todo professor de física ouve uma miríade de críticas a esse raciocínio, como se estivesse ensinando uma mentira, como se a realidade estivesse rindo da cara daqueles bloquinhos e polias, e muitas vezes está.
Não culpo o professor, este, se quisesse, poderia responder como Jack Nicholson a essa pergunta. Se um aluno reclama da incoerência do modelo com a realidade, que tente a realidade, vai voltar correndo a suas polias e bloquinhos. Porque a realidade é um monstro de complexidade e a física é feita de modelos: teorias que são tão boas quanto se propõem a ser. Ora, um cálculo de queda de objeto desprezando a resistência do ar funciona muito bem para quedas curtas, ou para objetos lançados na Lua, mas jamais se propôs a servir para lançar mísseis ou explicar o movimento de um paraquedista. Para esses fenômenos, você precisa de um modelo mais refinado, mais preciso; mas algo como um modelo exato não existe.
Como disse Weisskopf, modelos são como horários de trens na Áustria. Trens austríacos estão sempre atrasados. Um turista prussiano pergunta ao condutor austríaco por que eles se dão ao trabalho de imprimir essas tabelas, se os trens atrasam sempre. Ao que o condutor responde: “Se não as imprimíssemos, como saberíamos o quão atrasados eles estão?”.
E se você, com um ar levemente superior e arrogância não-desprezível, decidir criticar a ciência por “não saber nada exatamente”, eu pergunto: o que é saber algo exatamente? Eu posso descrever o movimento de minha cadeira, está parada, mas isso é apenas um modelo: há fótons bombardeando minha cadeira, interagindo com seus átomos, que por sua vez pulam, vibram, alguns até se soltam e voltam à cadeira, absorvem fótons, alguns até interagem com neutrinos de vez em quando, o wi-fi de minha casa atravessa a cadeira e interage com suas partículas, que também são bombardeadas pelas partículas de oxigênio e nitrogênio no ar. Essa cadeira, no nível atômico, é uma zona de guerra; descrever seu movimento, nesses termos, é um sonho tão distante quanto descrever o movimento de cada gota d’água em um tsunami. Se isso é saber algo, seriam necessários deuses para ensinar física ao ensino médio.
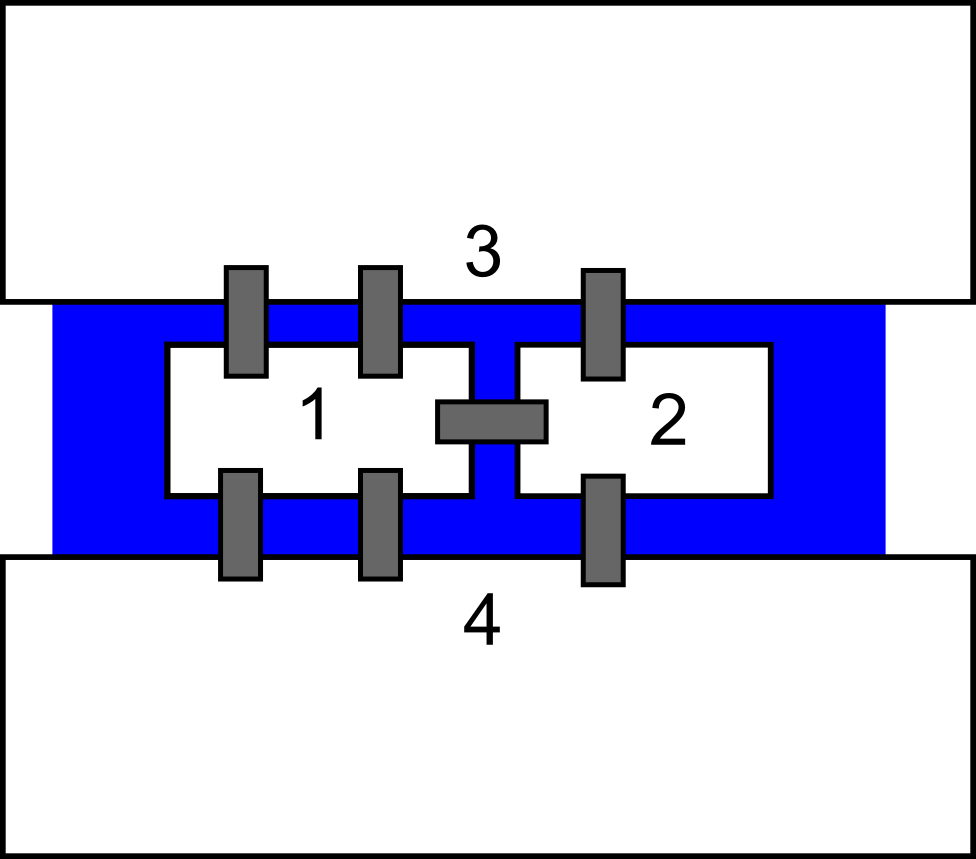
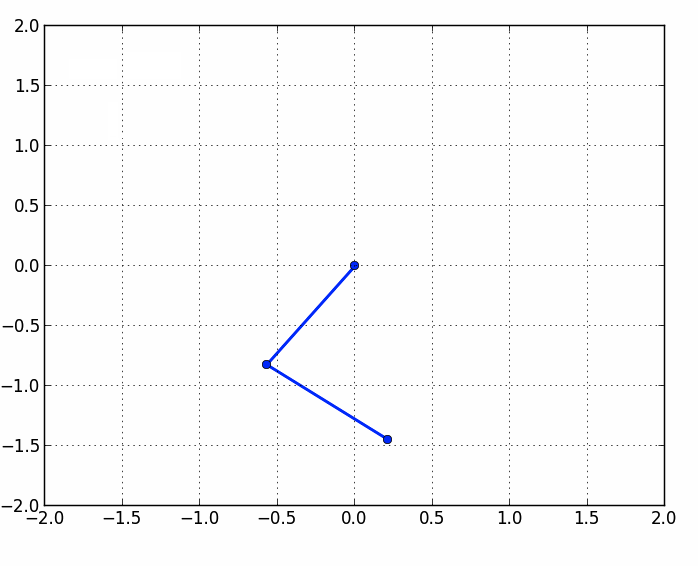
Nossos problemas não param por aí. Não somente realidade e modelos são coisas diferentes, muitas vezes nem nossos modelos ajudam. Ainda que tenhamos hipóteses bem otimistas, como a ausência da resistência do ar e do atrito, é terrivelmente fácil encontrar um sistema cuja solução é impossível aos mortais. E por impossível eu não digo “difícil” ou “eu não consigo porque sou moleque”, eu digo completamente impossível mesmo. Como exemplo, invoco o pêndulo duplo: uma bolinha presa por um fio em outra bolinha, presa por um fio em um ponto fixo. Algo com essa cara:
O problema desse sistema é: nem chorando você consegue prever o movimento dessas bolinhas. O sistema nada tem de aleatório, não há resistência do ar ou atrito, mas a relação entre as duas bolinhas, essa influência mútua causada pelo fio que as liga, torna o problema matematicamente tão complicado que ele toca as raias do impossível: não há homem sobre a terra capaz de escrever a coordenada $y$ de uma bolinha em função da $x$ para qualquer valor de tempo $t$.
O problema não é a física, você até conhece as equações desse problema. Lembra-se das leis de Newton?, pois bem, você consegue escrever o equivalente às leis de movimento das bolinhas. Essas leis, que são equações, se resolvidas, forneceriam a trajetória exata das bolinhas nesse modelo. O problema é: as equações não podem ser resolvidas exatamente, porque elas são equações muito difíceis.
Isso não nos impede, no entanto, de obter o movimento desse pêndulo estranho, basta explorar nosso amigo computador para isso. As equações são muito difíceis, impossíveis aos mortais no papel e caneta, mas o computador pode, na força bruta, calcular aos poucos cada instante dessa trajetória. Em cada momento, ele consegue estimar com bastante precisão onde o pêndulo estará no instante seguinte. Se esses instantes são bem próximos, a aproximação do computador é boa o suficiente para que o movimento seja descrito. Sentei essa tarde e escrevi um código para simular esse pêndulo, adaptando de outros que vi por aí, o resultado é algo perto disso:
E você também pode dizer que isso não é exato, essa nem é exatamente a resposta do modelo, e isso é verdade, em partes. Essas contas do computador são tão precisas quanto queremos que elas sejam, ora, basta você dizer o quão precisa você quer a conta que ele faz, vai apenas demorar mais ou menos tempo. Dessa maneira, esse pêndulo se movendo acima é preciso o suficiente para o que eu queria: um gif divertido que desse uma boa ideia do movimento do pêndulo.
O pêndulo duplo é um caso interessante por diversos motivos. Ele apresenta um fenômeno conhecido como caos, ou, na cultura popular, o efeito borboleta. Sistemas caóticos possuem definição matemática precisa e, como uma de suas características mais marcantes, possuem uma grande dependência de suas condições iniciais. No caso desse pêndulo duplo, dizemos que o lugar onde o pêndulo começa (no exemplo acima, a primeira bolinha forma um ângulo de 120º com a vertical, enquanto a segunda bolinha forma um ângulo de 10º com a vertical) influencia muito mais a trajetória do que você imagina.
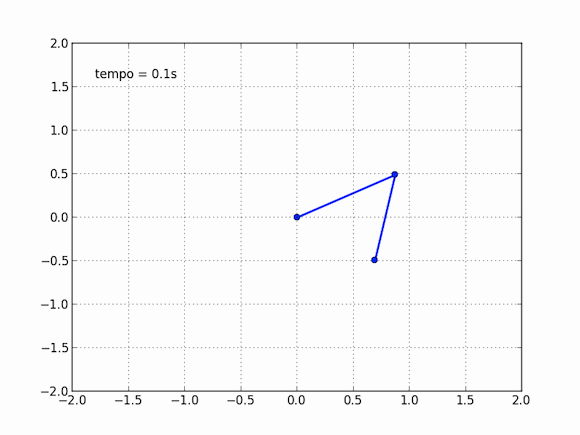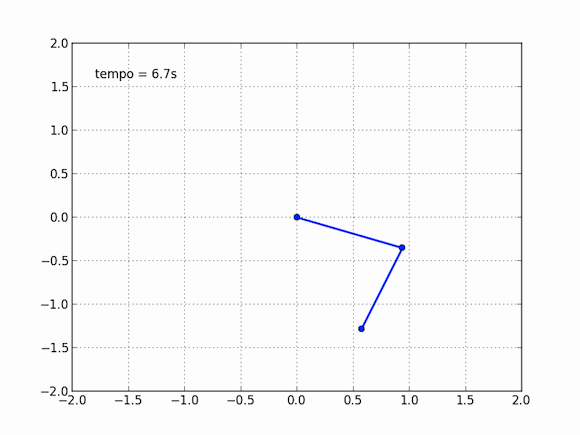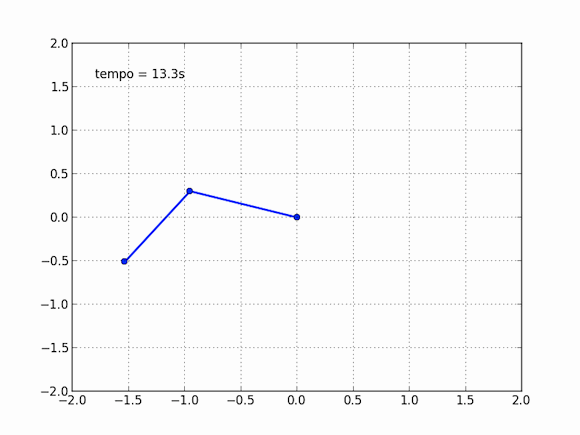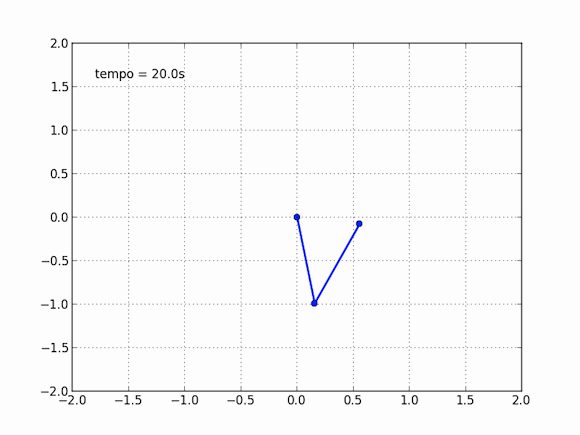
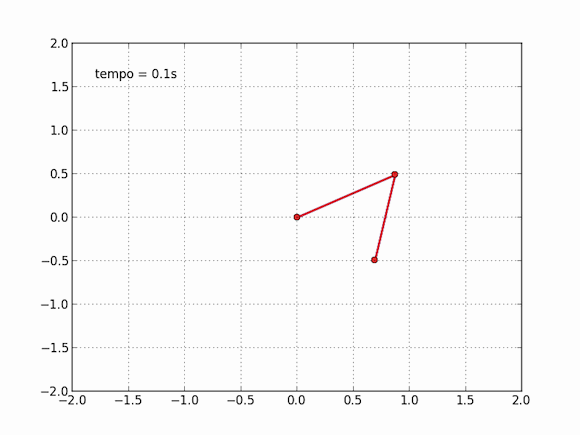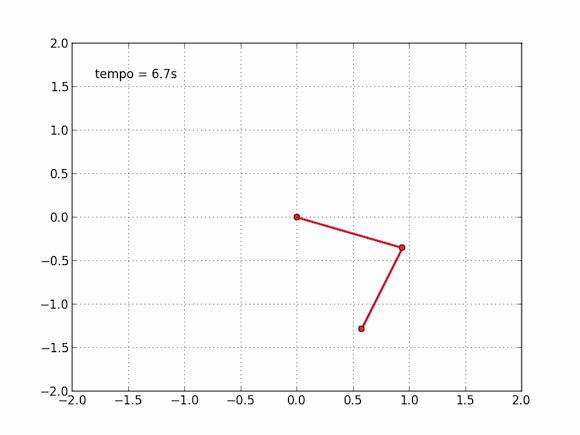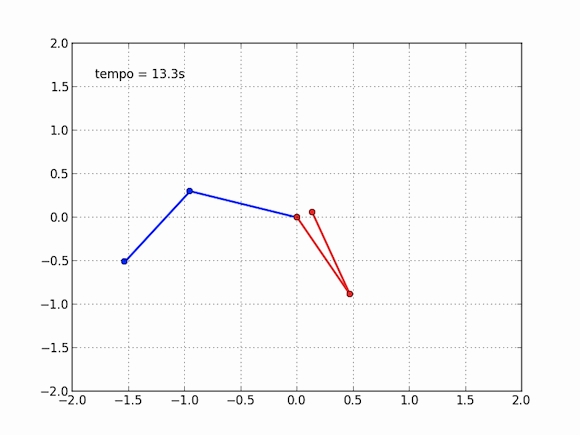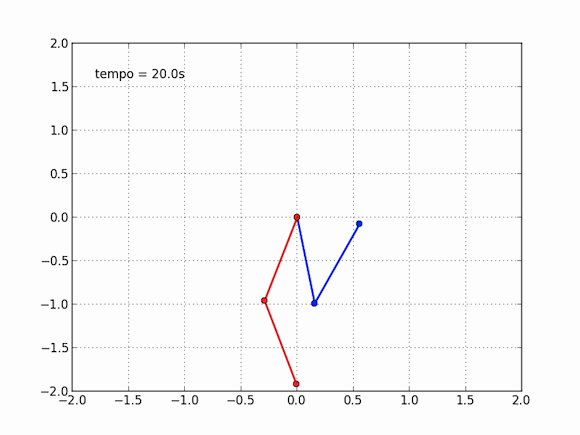
Compare com um pêndulo simples, indo de um lado a outro. Sua trajetória são será tão diferente se você lançar o pêndulo de um ângulo de 10° ou se lançar de 9,9999°, você, aliás, terá problemas para dizer se são diferentes. No pêndulo duplo, a história é outra. Para me divertir, repeti a animação com dois pêndulos ao mesmo tempo, um azul, como o anterior (120° na primeira e 10° na segunda), e um vermelho, com as configurações levemente alteradas (120° na primeira e 9,9999º na segunda). Veja o que acontece depois de um tempo suficientemente grande:
O efeito borboleta é uma possível interpretação dessa propriedade de sistemas caóticos. 10° e 9,9999° são muito próximos, mas em dez segundos os pêndulos passam a ser completamente diferentes, é impossível dizer que eles já estiveram juntos. Analogamente, as equações da mecânica dos fluidos são também muito difíceis de resolver, e apresentam comportamento caótico. Nesse pequeno gif, você percebe a influência de uma variação de 0,0001° na posição inicial de uma das bolinhas. Para a meteorologia, podemos perguntar: pode o bater de asas de uma borboleta no Brasil causar um tornado no Texas?
A ciência não pretende apresentar modelos completos que descrevem a realidade em todas as camadas e fronteiras, isso não existe. Ela pretende, contudo, descrever o que pode, na precisão que consegue, melhorando sempre, compreendendo mais e criando modelos mais precisos, tendo como única juíza a realidade. A ciência busca chegar à verdade e, nessa jornada, nossos trens chegam atrasados, é verdade; mas garanto, não há outros disponíveis.


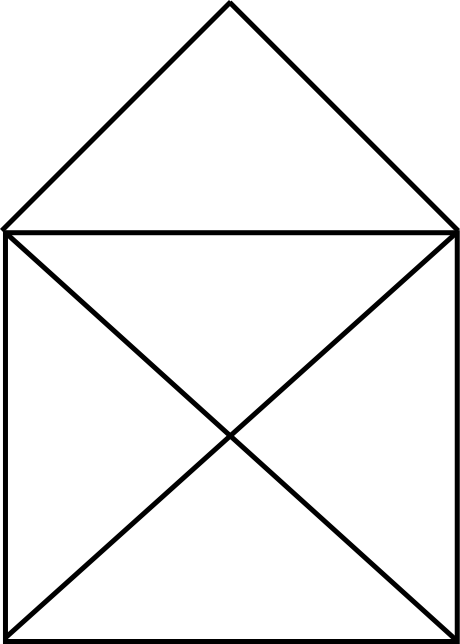
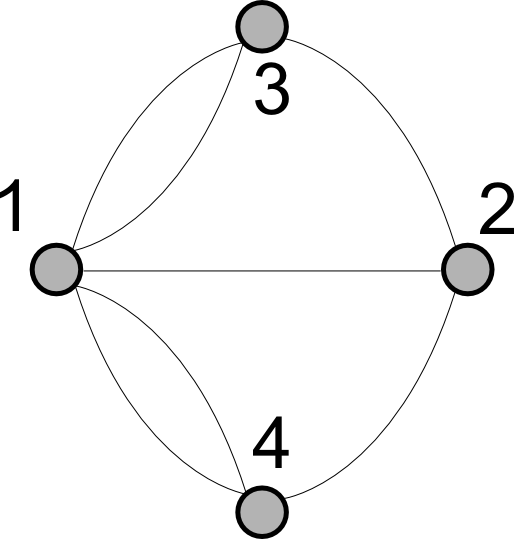
 E o desafio era atravessar as sete pontes sem repetir nenhuma. Você pode se divertir tentando, como os habitantes da cidade faziam, mas Euler decidiu pensar no problema de maneira mais profunda. A primeira coisa que fez foi se livrar do que estava sobrando: prédios, ilhas, estradas, apenas as pontes importavam:
E o desafio era atravessar as sete pontes sem repetir nenhuma. Você pode se divertir tentando, como os habitantes da cidade faziam, mas Euler decidiu pensar no problema de maneira mais profunda. A primeira coisa que fez foi se livrar do que estava sobrando: prédios, ilhas, estradas, apenas as pontes importavam: