Ricardo: O post de hoje é em inglês, e de um convidado muito especial. Alexander Dobrinevski, autor do blog inordinatum.wordpress.com, é meu grande amigo bielo-russo que, após sua graduação na Universidade Ludwig-Maximilians de Munique, seguiu para dois anos de mestrado em estudos avançados em matemática na Universidade de Cambridge e deu-me o privilégio de sua companhia no Laboratório de Física Teórica da École Normale Supérieure, onde dividimos sala durante alguns meses de trabalho enquanto ele fazia seu doutorado e eu, o mestrado. Viciado em cafés, filmes não tão mainstream e transformadas de Laplace. O post de hoje é bem hardcore, vale aos especialistas da área, e a mim, que aprendi e aprendo bastante a cada vez que nos falamos.

Ricardo: This post will be in english, for we have a very special guest today. Alexander Dobrinevski, author of the blog inordinatum.wordpress.com, is a good friend of mine from Belarus. Having finished his graduation at LMU, he followed the Advanced Studies in Mathematics program from Cambridge University to end up his doctoral thesis at the École Normale, where I had the pleasure to share with him the office for a few months. He is addicted to coffee, exotic movies and Laplace transforms. Today’s post is also very hardcore, to the benefit of our dear specialist in the field, and to mine, I who have learned so much and still do every time I get to talk to this dearest friend of mine.

---

Introduction

I guess anybody doing statistical physics or probability theory has played around with Brownian Motion (by which I mean, here and in the following, the Wiener process, and not the physical phenomenon) at some time or another. It is used e.g. for modelling the price of a stock, the position of a particle diffusing in a gas or liquid, or the pinning force on an elastic interface in a disordered medium.

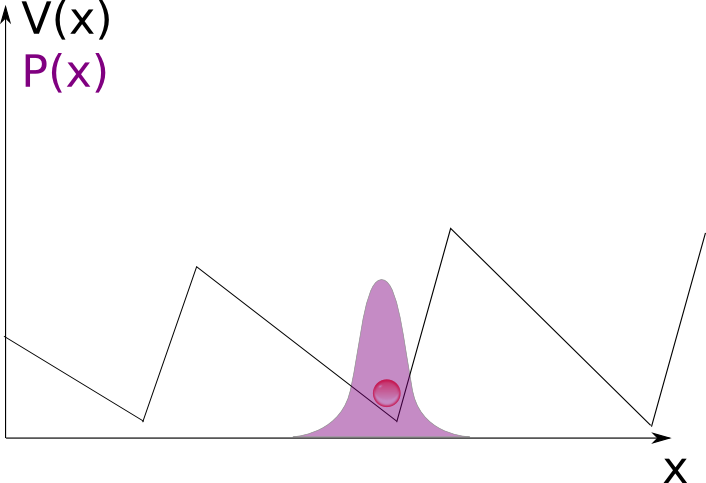
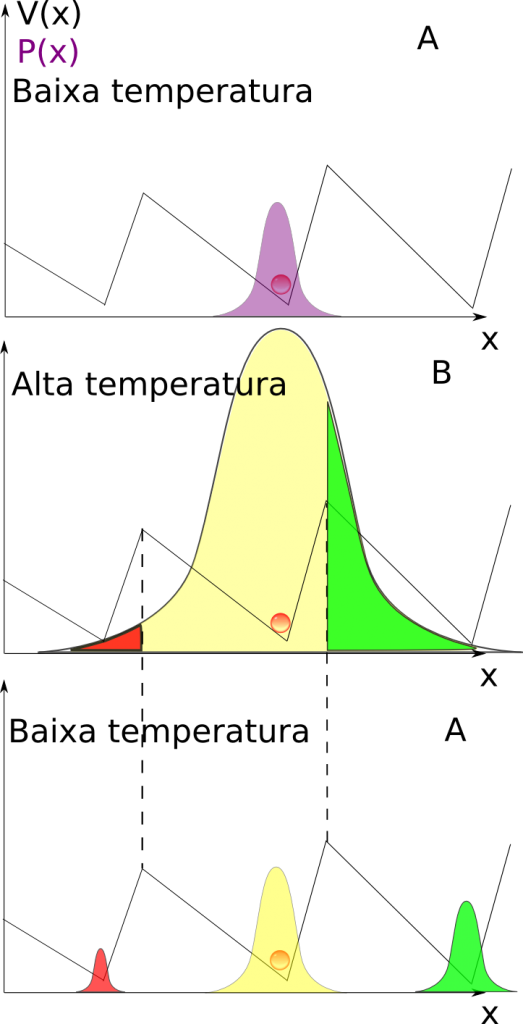
Being Markovian, time evolution of Brownian motion is completely determined by its propagator, i.e. the probability (density) to arrive at $x_1$ at time $ t_1$ starting from $ x_0$ at time $ t_0$. This is, of course, known to be a Gaussian. However, for practical applications, one often needs to restrict the Wiener process (in general, with drift) to a half-line or an interval, with some imposed boundary conditions (absorbing or reflecting). In the example of a stock price, these would describe call or put options on the stock. In this post I will derive, hopefully in a pedagogical way, the propagator of Brownian motion with drift and linear boundaries.

Propagators without drift

Let us first consider standard Brownian motion $ W(t)$ without drift. Without loss of generality, let us assume it starts at $W(0)=0$. It satisfies the Langevin equation

\[\dot{W}(t) = \xi(t)\]

where $ \xi(t)$ is Gaussian white noise with correlation

\[\overline{\xi(t)\xi(t’)} = 2\sigma \delta(t-t’).\]

With these conventions, the free propagator (i.e. the propagator without any boundaries) $ P(x,t)$ is given by the solution of the Fokker-Planck equation

\[ \partial_t P(x,t) = \sigma \partial_x^2 P(x,t)\]

with initial condition $ P(x,0) = \delta(x)$. This PDE, also known as the heat equation, is easily solved by taking a Fourier transform. The solution is given by

\[ P(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}e^{-\frac{x^2}{4\sigma t}}.\]

Now, let us determine the propagator with an absorbing boundary at $ x=b > 0$. In the Fokker-Planck equation, this is equivalent to the boundary condition $ P(b,t)=0$, which makes applying Fourier transforms difficult. However, we can use the method of images to find the solution: $ P(b,t)=0$ is enforced automatically if we add a negative source at $ x=2b$ (the position of the original source, reflected at $ b$), i.e. take the initial condition $ P(x,0) = \delta(x)-\delta(x-2b)$. The final propagator with an absorbing boundary at $ x=b$ is thus

\[P^{(b)}(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}\left[e^{-\frac{x^2}{4\sigma t}}-e^{-\frac{(x-2b)^2}{4\sigma t}}\right].\]

Similarly one can treat the case of two absorbing boundaries, one at $ x=b>0$, one at $ x=a<0$. One then needs an infinite series of images, and obtains the propagator as a series which can be rewritten in terms of Jacobi Theta functions.

Propagators with drift

Now let us generalize to the Brownian motion with drift $ \mu$. Then the Langevin equation for $ W(t)$ becomes

\[ \dot{W}(t) =\ mu + \xi(t).\]

The free propagator is obtained from the Fokker-Planck equation just as above:

\[P(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}e^{-\frac{(x-\mu t)^2}{4\sigma t}}.\]

Let us now introduce again a constant absorbing boundary at $ x=b$. Applying the method of images is not so straightforward anymore. Due to the drift, a path which goes from $ x=0$ to the boundary $ x=b$ will not have the same weight as the reflected path which goes from $ x=2b$ to the boundary $ x=b$. However, for the case of constant drift considered here, the weights of Brownian paths with and without drift have a simple relationship. In my view, the easiest way to see it is using path integrals. The propagator is given by

\[ P(x_f,t) = \int_{x(0)=0}^{x(t)=x_f} \mathcal{D}[x]e^{-\int_0^t \mathrm{d}s, \frac{1}{4\sigma}\left(\dot{x}(s)-\mu\right)^2}\]

Now, expanding the “action” in the exponent, using the fact that our drift $ \mu$ is constant, and using our boundary conditions, this is equal to

\[ P(x_f,t) = e^{-\frac{\mu}{2\sigma}x_f+ \frac{\mu^2}{4\sigma}t}\int_{x(0)=0}^{x(t)=x} \mathcal{D}[x]e^{-\int_0^t \mathrm{d}s, \frac{1}{2\sigma}\left(\dot{x}(s)\right)^2}.\]

We thus get a simple weight depending on the final position, but the remaining path integral is taken over a drift-less Brownian motion, and there we know the solution already, both with and without the boundary! In mathematical literature, you will often find this manipulation under the name of the Cameron-Martin-Girsanov theorem, but I find the path integral explanation much clearer for somebody coming from physics. Note that in the case where the drift $ \mu$ is a function of time, we cannot pull the weight out of the path integral, because it involves the whole trajectory and not just the final point. This shows why non-constant drift with absorbing boundaries is a much more complicated problem (although the free propagator is still trivial to write down!).

The final formula for the propagator of the Brownian motion with drift $ \mu$ and an absorbing boundary at $ x=b$ (also known as Bachelier-Levy formula) is thus

\[P^{(b,mu)}(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}e^{-\frac{mu}{2\sigma}x+ \frac{mu^2}{4\sigma}t}\left[e^{-\frac{x^2}{4\sigma t}}-e^{-\frac{(x-2b)^2}{4\sigma t}}\right]\]

This is now all that is required to compute things like first-passage times, survival probabilities, etc. The generalization to two absorbing boundaries follows from the solution in the driftless case by multiplying with the same weight as here.

I hope you see that with the right tools, obtaining these propagators is nothing miraculous. If you have any questions or comments, I’d be glad to hear them! If people are interested, at some point I may write a continuation of this blog post, possibly on generalizations of the methods discussed here to Ornstein-Uhlenbeck processes, Bessel Processes, or more complicated boundaries.

Have fun, and thanks for reading!

Ricardo: This post will be in english, for we have a very special guest today. Alexander Dobrinevski, author of the blog inordinatum.wordpress.com, is a good friend of mine from Belarus. Having finished his graduation at LMU, he followed the Advanced Studies in Mathematics program from Cambridge University to end up his doctoral thesis at the École Normale, where I had the pleasure to share with him the office for a few months. He is addicted to coffee, exotic movies and Laplace transforms. Today’s post is also very hardcore, to the benefit of our dear specialist in the field, and to mine, I who have learned so much and still do every time I get to talk to this dearest friend of mine.

---

Introduction

I guess anybody doing statistical physics or probability theory has played around with Brownian Motion (by which I mean, here and in the following, the Wiener process, and not the physical phenomenon) at some time or another. It is used e.g. for modelling the price of a stock, the position of a particle diffusing in a gas or liquid, or the pinning force on an elastic interface in a disordered medium.

Being Markovian, time evolution of Brownian motion is completely determined by its propagator, i.e. the probability (density) to arrive at $x_1$ at time $ t_1$ starting from $ x_0$ at time $ t_0$. This is, of course, known to be a Gaussian. However, for practical applications, one often needs to restrict the Wiener process (in general, with drift) to a half-line or an interval, with some imposed boundary conditions (absorbing or reflecting). In the example of a stock price, these would describe call or put options on the stock. In this post I will derive, hopefully in a pedagogical way, the propagator of Brownian motion with drift and linear boundaries.

Propagators without drift

Let us first consider standard Brownian motion $ W(t)$ without drift. Without loss of generality, let us assume it starts at $W(0)=0$. It satisfies the Langevin equation

\[\dot{W}(t) = \xi(t)\]

where $ \xi(t)$ is Gaussian white noise with correlation

\[\overline{\xi(t)\xi(t’)} = 2\sigma \delta(t-t’).\]

With these conventions, the free propagator (i.e. the propagator without any boundaries) $ P(x,t)$ is given by the solution of the Fokker-Planck equation

\[ \partial_t P(x,t) = \sigma \partial_x^2 P(x,t)\]

with initial condition $ P(x,0) = \delta(x)$. This PDE, also known as the heat equation, is easily solved by taking a Fourier transform. The solution is given by

\[ P(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}e^{-\frac{x^2}{4\sigma t}}.\]

Now, let us determine the propagator with an absorbing boundary at $ x=b > 0$. In the Fokker-Planck equation, this is equivalent to the boundary condition $ P(b,t)=0$, which makes applying Fourier transforms difficult. However, we can use the method of images to find the solution: $ P(b,t)=0$ is enforced automatically if we add a negative source at $ x=2b$ (the position of the original source, reflected at $ b$), i.e. take the initial condition $ P(x,0) = \delta(x)-\delta(x-2b)$. The final propagator with an absorbing boundary at $ x=b$ is thus

\[P^{(b)}(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}\left[e^{-\frac{x^2}{4\sigma t}}-e^{-\frac{(x-2b)^2}{4\sigma t}}\right].\]

Similarly one can treat the case of two absorbing boundaries, one at $ x=b>0$, one at $ x=a<0$. One then needs an infinite series of images, and obtains the propagator as a series which can be rewritten in terms of Jacobi Theta functions.

Propagators with drift

Now let us generalize to the Brownian motion with drift $ \mu$. Then the Langevin equation for $ W(t)$ becomes

\[ \dot{W}(t) =\ mu + \xi(t).\]

The free propagator is obtained from the Fokker-Planck equation just as above:

\[P(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}e^{-\frac{(x-\mu t)^2}{4\sigma t}}.\]

Let us now introduce again a constant absorbing boundary at $ x=b$. Applying the method of images is not so straightforward anymore. Due to the drift, a path which goes from $ x=0$ to the boundary $ x=b$ will not have the same weight as the reflected path which goes from $ x=2b$ to the boundary $ x=b$. However, for the case of constant drift considered here, the weights of Brownian paths with and without drift have a simple relationship. In my view, the easiest way to see it is using path integrals. The propagator is given by

\[ P(x_f,t) = \int_{x(0)=0}^{x(t)=x_f} \mathcal{D}[x]e^{-\int_0^t \mathrm{d}s, \frac{1}{4\sigma}\left(\dot{x}(s)-\mu\right)^2}\]

Now, expanding the “action” in the exponent, using the fact that our drift $ \mu$ is constant, and using our boundary conditions, this is equal to

\[ P(x_f,t) = e^{-\frac{\mu}{2\sigma}x_f+ \frac{\mu^2}{4\sigma}t}\int_{x(0)=0}^{x(t)=x} \mathcal{D}[x]e^{-\int_0^t \mathrm{d}s, \frac{1}{2\sigma}\left(\dot{x}(s)\right)^2}.\]

We thus get a simple weight depending on the final position, but the remaining path integral is taken over a drift-less Brownian motion, and there we know the solution already, both with and without the boundary! In mathematical literature, you will often find this manipulation under the name of the Cameron-Martin-Girsanov theorem, but I find the path integral explanation much clearer for somebody coming from physics. Note that in the case where the drift $ \mu$ is a function of time, we cannot pull the weight out of the path integral, because it involves the whole trajectory and not just the final point. This shows why non-constant drift with absorbing boundaries is a much more complicated problem (although the free propagator is still trivial to write down!).

The final formula for the propagator of the Brownian motion with drift $ \mu$ and an absorbing boundary at $ x=b$ (also known as Bachelier-Levy formula) is thus

\[P^{(b,mu)}(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}e^{-\frac{mu}{2\sigma}x+ \frac{mu^2}{4\sigma}t}\left[e^{-\frac{x^2}{4\sigma t}}-e^{-\frac{(x-2b)^2}{4\sigma t}}\right]\]

This is now all that is required to compute things like first-passage times, survival probabilities, etc. The generalization to two absorbing boundaries follows from the solution in the driftless case by multiplying with the same weight as here.

I hope you see that with the right tools, obtaining these propagators is nothing miraculous. If you have any questions or comments, I’d be glad to hear them! If people are interested, at some point I may write a continuation of this blog post, possibly on generalizations of the methods discussed here to Ornstein-Uhlenbeck processes, Bessel Processes, or more complicated boundaries.

Have fun, and thanks for reading!

Introduction

Quiconque ayant déjà pratiqué la physique statistique ou les probabilités a forcément eu affaire au mouvement Brownien (j’entends par là le processus de Wiener, et pas le phénomène physique). On l’utilise, par exemple, pour modéliser l’évolution des prix, la position des particules dans un liquide ou un gaz, ou la force d’ancrage sur l’interface élastique d’un milieu désordonné.

L’évolution temporelle du mouvement brownien est markovienne, et donc entièrement déterminée par son propagateur, c’est-à-dire la (densité de) probabilité d’atteindre $x_1$ à la date $ t_1$ en partant de $ x_0$ à la date $ t_0$. Il est bien connu que ce propagateur est gaussien. Cependant, pour des applications pratiques, il est souvent nécessaire de restreindre le processus de Wiener à une demi-droite ou un intervalle, avec des conditions aux bords imposées (absorption ou réflexion). Dans l’exemple du prix d’un stock, ces dernières décriront les options d’achat et de vente. Dans cet article, je vais obtenir le propagateur du mouvement brownien avec dérive et conditions aux bords linéaires, avec une approche que j’espère pédagogique.

Propagateurs sans dérive

Considérons d’abord le mouvement brownien standard $ W(t)$ sans dérive. Sans perte de généralité, supposons $W(0)=0$. $W$ vérifie l’équation de Langevin :

\[\dot{W}(t) = \xi(t)\]

où $ \xi(t)$ est un bruit blanc gaussien avec des corrélations

\[\overline{\xi(t)\xi(t’)} = 2\sigma \delta(t-t’).\]

Avec ces conventions, le propagateur libre (c’est-à-dire sans conditions aux bords) $ P(x,t)$ est donné par la solution de l’équation de Fokker-Planck

\[ \partial_t P(x,t) = \sigma \partial_x^2 P(x,t)\]

avec la condition initiale $ P(x,0) = \delta(x)$. Cette équation aux dérivées partielles, également connue sous le nom d’équation de la chaleur, se résout facilement en prenant une transformée de Fourier. On trouve

\[ P(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}e^{-\frac{x^2}{4\sigma t}}.\]

Maintenant, intéressons-nous au propagateur avec une frontière absorbante en $ x=b > 0$. Dans l’équation de Fokker-Planck, ceci se traduit par $ P(b,t)=0$, ce qui rend plus difficile la transformation de Fourier. Cependant, on peut utiliser la méthode des images pour trouver la position : $P(b,t)=0$ est automatique en ajoutant une source négative en $ x=2b$ (symétrique de la source initiale par rapport à la frontière en $ b$). Cela revient à prendre la condition initiale $ P(x,0) = \delta(x)-\delta(x-2b)$. Finalement, le propagateur avec frontière absorbante en  $x=b$ est

\[P^{(b)}(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}\left[e^{-\frac{x^2}{4\sigma t}}-e^{-\frac{(x-2b)^2}{4\sigma t}}\right].\]

On traite le cas de deux frontières absorbantes en $ x=b>0$ et $ x=a<0$ de la même façon, mais il faut maintenant une infinité d’images, et le propagateur s’écrit sous forme d’une série qui peut être exprimée en termes des fonctions $\vartheta$ de Jacobi.

Propagateurs avec dérive

Généralisons maintenant au mouvement brownien avec une dérive $ \mu$. L’équation de Langevin pour $ W(t)$ devient

\[ \dot{W}(t) =\ mu + \xi(t).\]

Comme ci-dessus, le propagateur libre se déduit de l’équation de Fokker-Planck :

\[P(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}e^{-\frac{(x-\mu t)^2}{4\sigma t}}.\]

Introduisons maintenant une frontière absorbante en $ x=b$. La méthode des images n’est plus évidente à appliquer ! A cause de la dérive, le poids d’une trajectoire partant de $ x=0$ vers la frontière en $ x=b$ ne sera pas le même que celui de son image, de $ x=2b$ à $ x=b$. Cependant, dans le cas d’une dérive constante, une relation simple lie les poids avec et sans dérive. Il me semble que la façon la plus simple de s’en rendre compte est l’utilisation des intégrales de chemin. Le propagateur est donné par

\[ P(x_f,t) = \int_{x(0)=0}^{x(t)=x_f} \mathcal{D}[x]e^{-\int_0^t \mathrm{d}s, \frac{1}{4\sigma}\left(\dot{x}(s)-\mu\right)^2}\]

En développant maintenant “l’action” dans l’exponentielle, et en utilisant le fait que $ \mu$est constant, ainsi que les conditions aux bords, on trouve

\[ P(x_f,t) = e^{-\frac{\mu}{2\sigma}x_f+ \frac{\mu^2}{4\sigma}t}\int_{x(0)=0}^{x(t)=x} \mathcal{D}[x]e^{-\int_0^t \mathrm{d}s, \frac{1}{2\sigma}\left(\dot{x}(s)\right)^2}.\]

On obtient alors un poids qui ne dépend que de la position finale (hors de l’intégrale), et l’intégrale restante ne présente plus de dérive, ce qui signifie que nous connaissons déjà la solution, avec ou sans frontières ! Dans la littérature mathématique, vous trouverez fréquemment cette manipulation sous le nom de “Théorème de Cameron-Martin-Girsanov“, mais je trouve que l’approche via l’intégrale de chemin est beaucoup plus claire pour un physicien. Notons que si la dérive $ \mu$ dépend du temps, on ne peut pas sortir le poids de l’intégrale de chemin, car il dépend de toute la trajectoire, et pas seulement du point final. C’est pourquoi il s’agit d’un problème bien plus difficile, bien que le propagateur libre soit toujours trivial à écrire !

La formule finale pour le propagateur du mouvement brownien avec dérive $ \mu$ et une frontière absorbante en $ x=b$ (connu sous le nom de “formule de Bachelier-Levy”) est donc

\[P^{(b,mu)}(x,t) = \frac{1}{\sqrt{4\pi\sigma t}}e^{-\frac{mu}{2\sigma}x+ \frac{mu^2}{4\sigma}t}\left[e^{-\frac{x^2}{4\sigma t}}-e^{-\frac{(x-2b)^2}{4\sigma t}}\right]. \]

C’est tout ce dont nous avons besoin pour calculer des choses comme des temps de premier passage, des probabilités de survie, etc. La généralisation à deux frontières absorbantes peut être déduite de la solution sans dérive, en multipliant par le même poids.

J’espère vous avoir fait sentir qu’avec les bons outils, obtenir ces propagateurs n’a rien de miraculeux. Si vous avez des questions ou des commentaires, je serai ravi de les entendre ! Pour approfondir, diverses voies sont envisageables, comme des généralisations des méthodes exposées ici aux processus de Ornstein-Uhlenbeck, de Bessel, ou encore des conditions aux bords plus compliquées.

Merci de m’avoir lu !